Finite Difference Methods For Poisson Equations
Poisson's equation: Poisson's equation is a second-order partial differential equation which arises in physical problems such as finding the electric potential of a given charge distribution.
Consider the solution of the Poisson’s equation
uxx uyy = ∇2u = G(x, y),.................1.1
with u(x, y) prescribed on the boundary, that is, u(x, y) = g(x, y) on the boundary.
Then equation
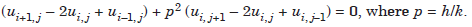
And
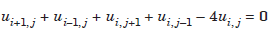
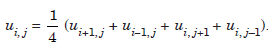
become
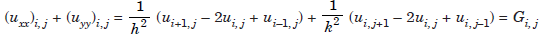..................1.2
or,
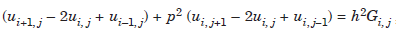....................1.3
where
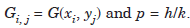
If h = k, that is, p = 1, we obtain the difference approximation as
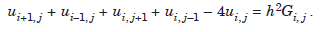................1.4
This approximation is called the standard five point formula for Poisson’s equation. The formula (1.3) is of order O(h2 k2) and formula (1.4) is of order O(h2). We also call it a second order formula.
When h = k, the diagonal five point formula for solving the Poisson’s equation can be written as
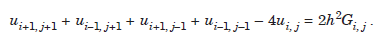.................1.5