Gauss Three Point Rule (Gauss-legendre Three Point Rule)
Gauss Three point rule (Gauss-Legendre Three point rule) : The three point rule is given by
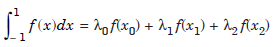
where λ0 ≠ 0, λ1 ≠ 0, λ2 ≠ 0, and x0 ≠ x1 ≠ x2. The method has six unknowns λ0, x0, λ1, x1, λ2, x2.
Making the formula exact for f(x) = 1, x, x2, x3, x4, x5, we get
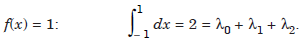...................1.1
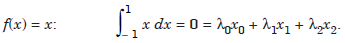.................1.2
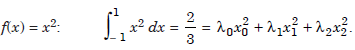...................1.3
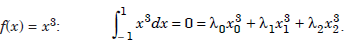....................1.4
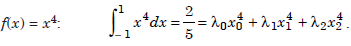........................1.5
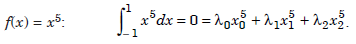.....................1.6
Solving this system as in the two point rule, we obtain
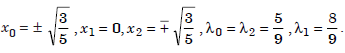
Therefore, the three point Gauss rule (Gauss-Legendre rule) is given by
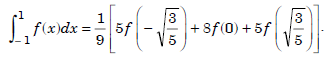...................1.7
Error of approximation :
The error term is obtained when f(x) = x6. We obtain
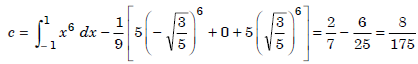
The error term is given by
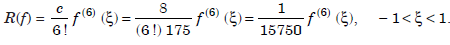
Note : Since the error term contains f (6)(ξ), Gauss three point rule integrates exactly polynomials of degree less than or equal to 5. Further, the error coefficient is very small (1/15750 ≈ 0.00006349). Therefore, the results obtained from this rule are very accurate. We have not derived any Newton-Cotes rule, which can be compared with the Gauss three point rule. If better accuracy is required, then the original interval [a, b] can be subdivided and the limits of each subinterval can be transformed to [– 1, 1]. Gauss three point rule can then be applied to each of the integrals