Gauss Two Point Rule (Gauss-legendre Two Point Rule)

Gauss Two point rule (Gauss-Legendre Two point rule) :

The two point rule is given by

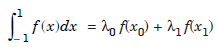
where λ₀ ≠ 0, λ₁ ≠ 0 and x₀ ≠ x1. The method has four unknowns λ₀, x₀, λ₁, x₁. Making the
formula exact for f(x) = 1, x, x², x³

^{We get,}

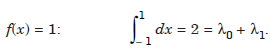......................1.1

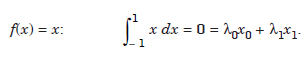.....................1.2

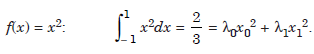.....................1.3

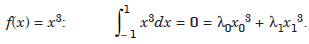.......................1.4

Eliminating λ0 from (1.2) and (1.4), we get

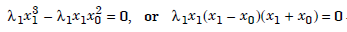
Now, λ₁ ≠ 0 and x₀ ≠ x₁. Hence, x₁ = 0, or x₁ = – x₀. If x₁ = 0, (1.2) gives x₀ = 0, which is not possible. Therefore, x₁ = – x₀.

Substituting in (1.2), we get 

λ₀ – λ₁ = 0, or λ₀ = λ₁.

Substituting in (1.3), we get

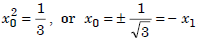
Therefore, the two point Gauss rule (Gauss-Legendre rule) is given by

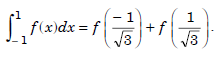........................1.5

Error of approximation

The error term is obtained when f(x) = x⁴. We obtain

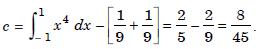
The error term is given by

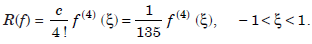.......................1.6