Introduction To Initial Value Problem For Ordinary Differential Equations
Initial Value problems :
The initial value problem for an ordinary differential equation entails finding a function u(t) that satisfies the differential equation
φ(x, y, y′, y″, ..., y(m)) = 0....................1.1
Where m is the order of the a differential equation.
The order of a differential equation is the order of its highest order derivative and the degree is the degree of the highest order derivative after the equation has been rationalized in derivatives. A linear differential equation of order m can be written as
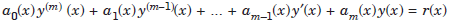..................1.2
where a0(x), a1(x), ..., am (x) and r(x) are constants or continuous functions of x.
The general solution of the equations (1.1) or (1.2) contains m arbitrary constants. The solution may be obtained in an implicit form as
g(x, y, c1, c2, ..., cm) = 0,................1.3
or in an explicit form as
y = h(x, c1, c2, ..., cm)...................1.4
The m arbitrary constants c1, c2, ..., cm can be determined by prescribing m conditions of the form
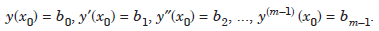......................1.5
The conditions are prescribed at one point x0. This point x0 is called the initial point and the conditions (1.5) are called initial conditions. The differential equation (1.1) or (1.2) together with the initial conditions (1.5) is called an initial value problem. A first order initial value problem can be written as
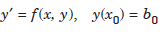....................1.6