Iterative Methods
iterative methods are based on the idea of successive approximations. We start with an initial approximation to the solution vector x = x0, to solve the system of equations Ax = b, and obtain a sequence of approximate vectors x0, x1, ..., xk, ..., which in the limit as k → ∞, converges to the exact solution vector x = A-1b. A general linear iterative method for the solution of the system of equations Ax = b, can be written in matrix form as
x(k 1)= Hx(k) c, k = 0, 1, 2, …................1.1
where x(k 1) and x(k) are the approximations for x at the (k 1)th and kth iterations respectively. H is called the iteration matrix, which depends on A and c is a column vector, which depends on A and b.
When to stop the iteration We stop the iteration procedure when the magnitudes of the differences between the two successive iterates of all the variables are smaller than a given accuracy or error tolerance or an error bound ε, that is,
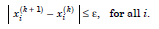......................1.2
For example, if we require two decimal places of accuracy, then we iterate until
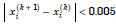for all i
If we require three decimal places of accuracy, then we iterate until
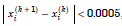for all i
Convergence property of an iterative method depends on the iteration matrix H.
Now, we derive two iterative methods for the solution of the system of algebraic equations
.........................1.3