Milne-simpsons Method

Milne-Simpsons Method : It is a numerical method which involve Simpson's rule  for solving a linear differential equation.

 

To derive the Milne’s methods, we integrate the differential equation y′ = f(x, y) in the interval [x_i–1, x_{i 1}]. We get

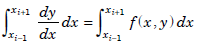
or,

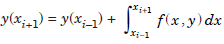..................1.1

 

To derive the methods, we use the same approximation, follow the same procedure and steps as in Adams-Moulton methods. The interval of integration for s is

[– 1, 1]. We obtain

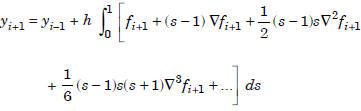
now,

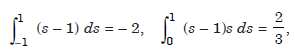
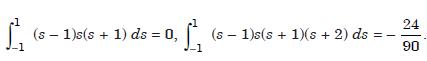
Hence, we have

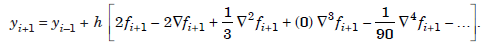.....................1.2

These methods are called Milne’s methods.

The case k = 2, is of interest for us. We obtain the method as

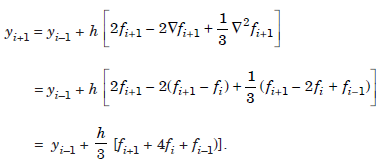.....................1.3

This method is also called the Milne-Simpson’s method.

For using the method, we require the starting values y_i, y_i–1.

The error term is given by

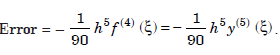
Therefore, the method is of fourth order.

 

Note :

The methods derived in this section are all implicit methods. Therefore, we needto solve a nonlinear algebraic equation for obtaining the solution at each point. Hence, these methods are not used as such but in combination with the explicit methods. This would give rise to the explicit-implicit methods or predictor-corrector methods, which we describe in the next section.