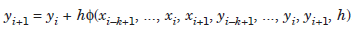Multi Step Methods

Multi step Methods:

Linear multistep methods are used for the numerical solution of ordinary differential equations.

In multi step methods, the solution at any point xi 1 is obtained using the solution at a number of previous points. Suppose that we use y(x) and y′(x) at k 1 previous points x_{i 1} , x_i, x_i–1, ..., x_{i–k 1}. That is, the values

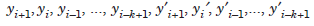
are used to determine the approximation to y(x) at x_{i 1}. We assume that the numerical solution is being obtained at x_{i 1} and the solution values at all the required previous points are known. We call the method as a k-step multi step method

For example, a two step method uses the values y_{i 1}, y_i, y_i–1, y′_{i 1}, y_i′, y′_i–1 and the method can be written as

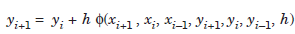
or

 

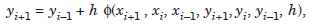
where φ depends on the right hand side f(x, y) of the given differential equation. This function φ is called the increment function.

If y_{i 1} can be obtained simply by evaluating the right hand side, then the method is called an explicit method. In this case, the two step method is of the form

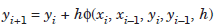
or

 

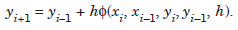
If the right hand side depends on y_{i 1} also, then it is called an implicit method, that is,we obtain a nonlinear algebraic equation for the solution of y_{i 1} (if the differential equation isnonlinear).

A general k-step explicit method can be written as

 

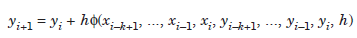
and a general k-step implicit method can be written as