Multi Step Methods And Predictor-corrector Methods

Multi Step Methods  :   Linear multistep methods are used for the numerical solution of ordinary differential equations.

As we discussed the multi step method.we have defined the explicit and implicit multi step methods for the solution of the initial value problem.

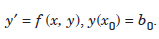............1.1

A general k-step explicit method can be written as

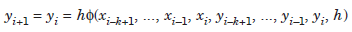...................1.2

 

Note :

1.Multi step methods are not self starting.

 

2.since a k-step multi step method requires the k previous values y_i, y_i–1, ..., y_{i–k 1}.

 

3.The k values that are required for starting the application of the method are obtained by using some single step method like Euler’s method, Taylo series method or Runge-Kutta method, which is of the same or lower order than the order of the multi step method.

 

Let us construct a few multi step methods.

Integrating the differential equation y′ = f(x, y) in the interval [x_i, x_{i 1}], we get

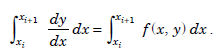
or,

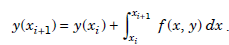..................1.1

To derive the methods, we approximate the integrand f(x, y) by a suitable interpolation polynomial.

In general, we may integrate the differential equation y′ = f(x, y) in the interval [x_i–m, x_{i 1}]. We get

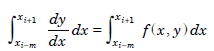
or

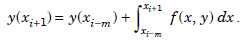
For m = 0,