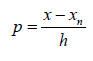Newton's Backward Difference Interpolation Formula
For interpolating the value of the function y = f (x) near the end of table of values, and to extrapolate value of the function a short distance forward from yn, Newton’s backward interpolation formula is used.
Derivation:
Let y = f (x) be a function which takes on values.
f (xn), f (xn-h), f (xn-2h), …, f (x0) corresponding to equispaced values xn, xn-h, xn-2h,…, x0. Suppose, we wish to evaluate the function f (x) at (xn ph), where p is any real number, then we have the shift operator E, such that
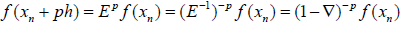
Binomial expansion yields,
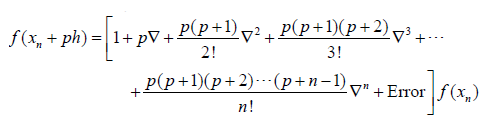
That is
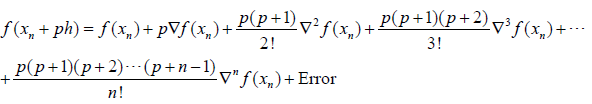
This formula is known as Newton’s backward interpolation formula. This formula is also known as Newton’s-Gregory backward difference interpolation formula. If we retain (r 1)terms, we obtain a polynomial of degree r agreeing with f (x) at xn,xn-1, …, xn-r. Alternatively, this formula can also be written as
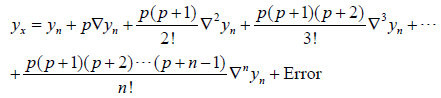
Here