Newtons Divided Difference Interpolation

The Newton's divided difference interpolation is used to find higher order divided difference.

 

We write the interpolating polynomial as

              

                                                         f(x) = P_n(x)   =    c₀ (x – x₀) c₁ (x – x₀)(x – x₁) c₂ ... (x – x₀)(x – x₁)...(x – x_n-1) c_n.  ....................1.1

The polynomial fits the data                                                                                 Pn(xi) = f(x_i) = f_i

Setting                                                                                                                      P_n(x₀) = f₀,

we obtain

Pn(x₀) = f₀ = c₀

since all the remaining terms vanish.

Setting P_n(x₁) = f₁, we obtain

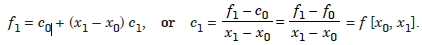
Setting P_n(x₂) = f₂, we obtain

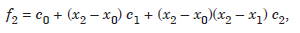
or

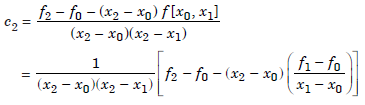
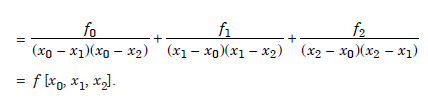
By induction, we can prove that

cn = f [x₀, x₁, x₂, ..., x_n].

Hence, we can write the interpolating polynomial as

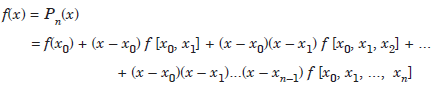....................1.2

 

This polynomial is called the Newton’s divided difference interpolating polynomial.