Power Method
This method is used to find the largest eigen value in magnitude and the corresponding eigen vector of eigen value problem Ax = λ x is called power method.
The necessary and sufficient condition for convergence of the Gauss-Jacobi and Gauss-Seidel iteration methods is that the spectral radius of the iteration matrix H is less than one unit, that is, ρ(H) < 1, where ρ(H) is the largest eigen value in magnitude of H. If we write the matrix formulations of the methods, then we know H. We can now find the largest eigen value in magnitude of H, which determines whether the methods converge or not.
We assume that λ1, λ2,..., λn are distinct eigen values such that
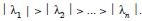.....................1.1
Let v1, v2,..., vn be the eigen vectors corresponding to the eigen values λ1, λ2,..., λn, respectively. The method is applicable if a complete system of n linearly independent eigen vectors exist, even though some of the eigen values λ2, λ3,..., λn, may not be distinct. The n linearly independent eigen vectors form an n-dimensional vector space. Any vector v in this space of eigen vectors v1, v2,..., vn can be written as a linear combination of these vectors. That is,
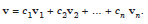..................1.2
Premultiplying by A and substituting Av1 = λ1v1, Av2 = λ2v2,..., Avn = λnvn, we get
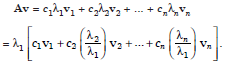
Premultiplying repeatedly by A and simplifying, we get
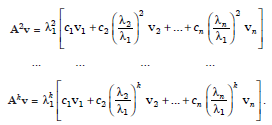....................1.3
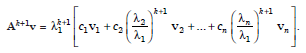....................1.4
as k→∞ the right hand side of equation 1.3 and 1.4 tends to
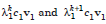
since
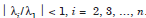
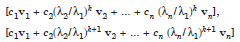
tend to c1v1, which is the eigen vector corresponding to λ1. The eigen value λ1 is obtained as the ratio of the corresponding components of Ak 1v and Akv. That is,
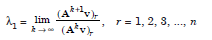..................1.5
where the suffix r denotes the rth component of the vector. Therefore, we obtain n ratios, all of them tending to the same value, which is the largest eigen value in magnitude,
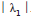
When do we stop the iteration The iterations are stopped when all the magnitudes of the differences of the ratios are less than the given error tolerance.