Romberg Method For The Trapezium Rule
Neglecting the O(h4) error term, we obtain the new approximation to the value of the integral as
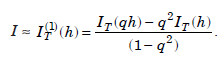..........................1.8
We note that this value is obtained by suitably using the values of the integral obtained with step lengths h and qh, 0 < q < 1. This computed result is of order, O(h4), which is higher than the order of the trapezium rule, which is of O(h2).
For q = 1/2, that is, computations are done with step lengths h and h/2, the formula (1.8) simplifies to
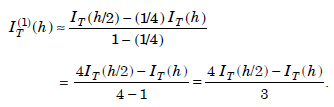..........................1.9
In practical applications, we normally use the sequence of step lengths h, h/2, h/22, h/23, ...
Suppose, the integral is computed using the step lengths h, h/2, h/22. Using the results obtained with the step lengths h/2, h/22, we get
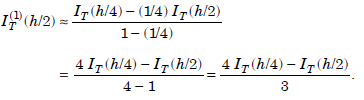........................2.0
Both the results IT(1)(h), IT(1) (h/2) are of order, O(h4). Now, we can eliminate the O(h4) terms of these two results to obtain a result of next higher order, O(h6). The multiplicative factor is now (1/2)4 = 1/16. The formula becomes
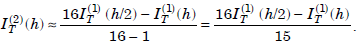............................2.1
Therefore, we obtain the Romberg extrapolation procedure for the composite trapezium rule as
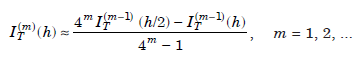.............................2.2
where,
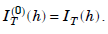
The computed result is of order O(h2m 2).
The extrapolations using three step lengths h, h/2, h/22, are given in Table 3.1.
Figure : Romberg method for trapezium rule