Runge-kutta Fourth Order Method

Runge-Kutta Fourth Order Method : A method of numerically integrating ordinary differential equations by using a trial step at the midpoint of an interval to cancel out lower-order error terms

In vector format, we write the Runge-Kutta fourth order method (4.51) as

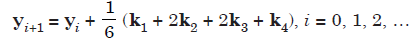....................1.1

where,

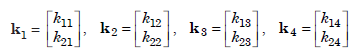....................1.2

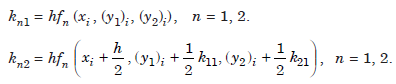
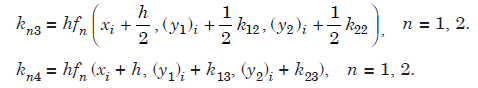
Note that we have used the matrix notation for representing the column vectors k₁, k₂,k₃, k₄. Some books use the notation (k₁, l₁), (k₂, l₂), (k₃, l₃), (k₄, l₄) for representing the columnvectors k₁, k₂, k₃, k₄.

In explicit form, we write the method as

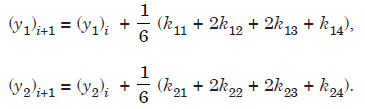
If we denote y₁ = u, y₂ = v, then we can write the equations as

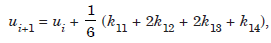...................1.3

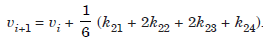...................1.4