Single Step Method

Single Step Method : A single step process is examined for a linear differential equation of order n. Conditions are derived which constrain the parameters of the process and which are necessary to give methods of specified order. A simple set of sufficient conditions is obtained.

In single step methods, the solution at any point x_{i 1} is obtained using the solution at only the previous point x_i. Thus, a general single step method can be written as

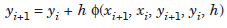....................1.1

where φ is a function of the arguments x_{i 1}, x_i, y_{i 1}, y_i, h and depends on the right hand side f(x, y) of the given differential equation. This function φ is called the increment function.

If y_{i 1} can be obtained simply by evaluating the right hand side of (1.1), then the methodis called an explicit method. In this case, the method is of the form

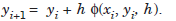...............1.2

That is, we compute successively

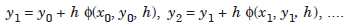
If the right hand side of (1.1) depends on y_{i 1} also, then it is called an implicit method, that is, we obtain a nonlinear algebraic equation for the solution of y_{i 1} (if the differential equation is nonlinear.

Local truncation error or discretization error The exact solution y(xi) satisfies the equation

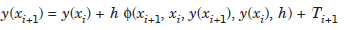...................1.3

where T_{i 1} is called the local truncation error or discretization error. Therefore, the Truncation error (T.E.) is defined by

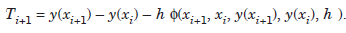.......................1.4

Order of a method The order of a method is the largest integer p for which

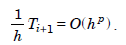....................1.5