Solution Of Algebraic And Transcendental Equations
Introduction:
A problem of great importance in science and engineering is that of determining the roots/zeros of an equation of the form
f(x) = 0,....................... (1.1)
A polynomial equation of the form
f(x) = Pn(x) = a0xn a1xn–1 a2xn–2 ... an –1x an = 0 .....................(1.2)
is called an algebraic equation. An equation which contains polynomials, exponential functions,logarithmic functions, trigonometric functions etc. is called a transcendental equation.
For example,
3x3 – 2x2 – x – 5 = 0, x4 – 3x2 1 = 0, x2 – 3x 1 = 0,
are algebraic (polynomial) equations,
and
xe2x – 1 = 0, cos x – xex = 0, tan x = x
are transcendental equations.
We assume that the function f(x) is continuous in the required interval.
Root/zero A number α, for which f(α) ≡ 0 is called a root of the equation f(x) = 0, or a zero of f(x). Geometrically, a root of an equationn f(x) = 0 is the value of x at which the graph of the equation y = f(x) intersects the x-axis (see Figure 1.1)
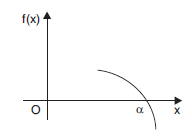
Figure 1.1
Simple root A number α is a simple root of f(x) = 0, if f(α) = 0 and f ′(α) ≠ 0. Then, we can write f(x) as
f(x) = (x – α) g(x), g(α) ≠ 0...................(1.3)
For example, since (x – 1) is a factor of f(x) = x3 x – 2 = 0, we can write
f(x) = (x – 1)(x2 x 2) = (x – 1) g(x), g(1) ≠ 0.
Alternately, we find f(1) = 0, f ′(x) = 3x2 1, f ′(1) = 4 ≠ 0. Hence, x = 1 is a simple root of
f(x) = x3 x – 2 = 0.
Multiple root A number α is a multiple root, of multiplicity m, of f(x) = 0, if
f(α) = 0, f ′(α) = 0, ..., f (m –1) (α) = 0, and f (m) (α) ≠ 0. .....................(1.4)
Then, we can write f(x) as
f(x) = (x – α)m g(x), g(α) ≠ 0.
For example, consider the equation f(x) = x3 – 3x2 4 = 0. We find
f(2) = 8 – 12 4 = 0, f ′(x) = 3x2 – 6x, f ′(2) = 12 – 12 = 0,
f ″(x) = 6x – 6, f ″(2) = 6 ≠ 0.
Hence, x = 2 is a multiple root of multiplicity 2 (double root) of f(x) = x3 – 3x2 4 = 0.
We can write f(x) = (x – 2)2 (x 1) = (x – 2)2 g(x), g(2) = 3 ≠ 0