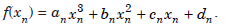Spline Function

An interpolation method in which cell values are estimated using a mathematical function that minimizes overall surface curvature, resulting in a smooth surface that passes exactly through the input points.

A spline function consists of polynomial pieces on subintervals joined together with certain continuity conditions. Formally, suppose that n 1 points

t₀, t₁, · · · , t_n have been specified and satisfy t₀ < t₁ < · · · < t_n

These points are called knots.

A spline of degree 0 can be given explicitly in the form

 

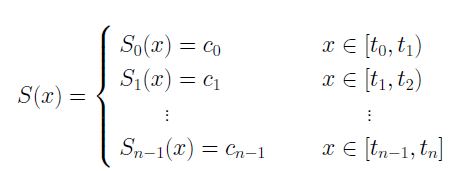
The intervals [t_i-1, t_i) do not intersect each other, and so no ambiguity arises in defining such a function at the knots.

A spline function of degree n with nodes x₀, x₁, ..., x_n, is a function F(x) satisfying the following properties.

(i) F(xi) = f(x_i), i = 0, 1, ...., n. (Interpolation conditions).

(ii) On each subinterval [x_i-1, x_i], 1 ≤ i ≤ n, F(x) is a polynomial of degree n.

(iii) F(x) and its first (n – 1) derivatives are continuous on (a, b).

On each interval, we have four unknowns a_i, b_i, c_i and d_i, i = 1, 2, ..., n. Therefore, the total number of unknowns is 4n.

Continuity of F(x), F′(x) and F″(x) on (a, b) implies the following.

(i) Continuity of F(x) :

On

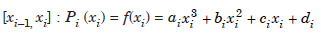
On

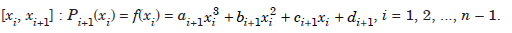
(ii) Continuity of F′(x) :

 

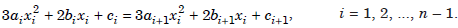
(iii) Continuity of F″ (x) :

At the end points x₀ and x_n, we have the interpolation conditions

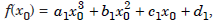
and