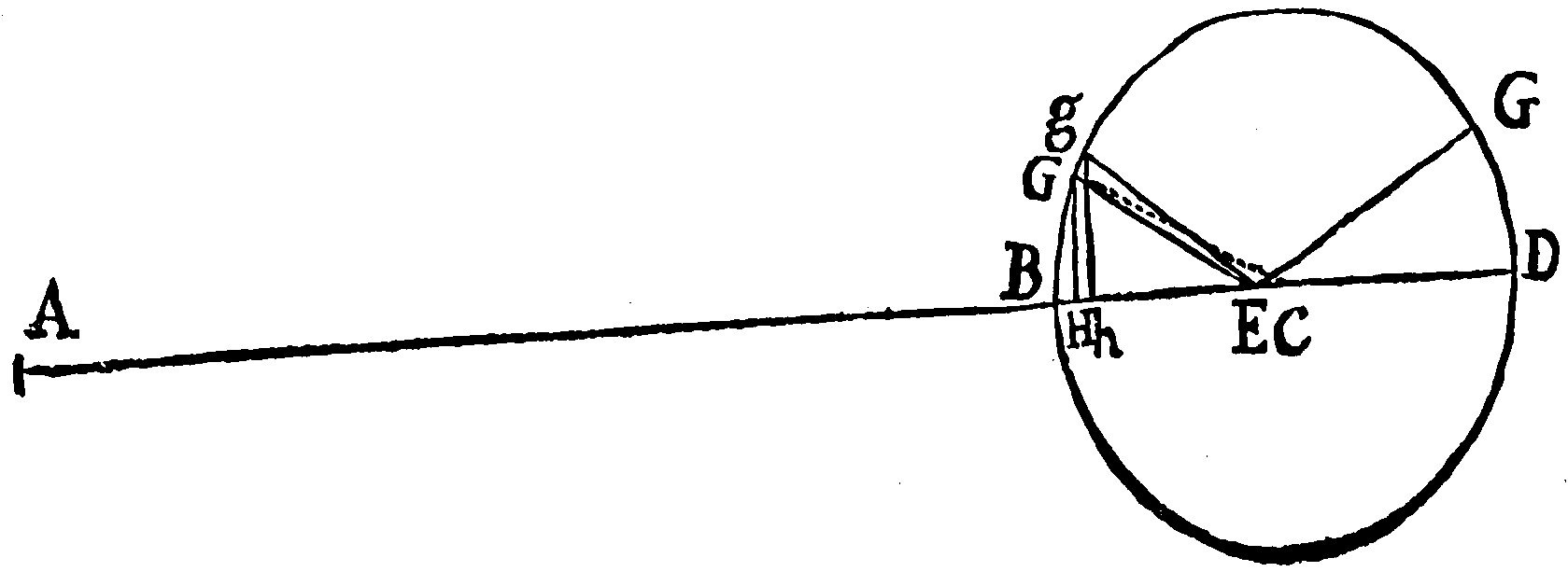Designet S Solem, T Terram, P Lunam, NPn Orbem Lunæ, Npn vestigium Orbis in plano Eclipticæ; N, n, Nodos, nTNm lineam Nodorum infinitè productam, PI, PK; perpendicula demissa in lineas ST, Qq; Pp perpendiculum demissum in planum Eclipticæ; Q, q Quadraturas Lunæ in plano Eclipticæ & pK perpendiculum in lineam Qq Quadraturis intrajacentem. Et vis Solis ad perturbandum motum Lunæ (per Prop. XXV.) duplex erit, altera lineæ 2IT vel 2Kp, altera lineæ PI proportionalis. Et Luna vi priore in Solem, posteriore in lineam ST trahitur. Componitur autem vis posterior PI ex viribus IT & PT, quarum PT agit secundum planum orbis Lunaris, & propterea situm plani nil mutat. Hæc igitur negligenda est. Vis autem IT cum vi 2IT componit vim totam 3IT, qua planum Orbis Lunaris perturbatur. Et hæc vis per Prop. XXV. est ad vim qua Luna in circulo circa Terram quiescentem tempore suo periodico revolvi posset, ut 3IT ad Radium circuli multiplicatum per numerum 178,725, sive ut IT ad Radium multiplicatum per 59,575. Cæterum in hoc calculo & eo omni qui sequitur, considero lineas omnes à Luna ad Solem ductas tanquam parallelas lineæ quæ à Terra ad Solem ducitur, propterea quod inclinatio tantum ferè minuit effectus omnes in aliquibus casibus, quantum auget in aliis; & Nodorum motus mediocres quærimus, neglectis istiusmodi minutiis, quæ calculum nimis impeditum redderent.

Designet jam PM arcum, quem Luna dato tempore quam minimo describit, & ML lineolam quam Luna, impellente vi præfata 3IT, eodem tempore describere posset. Jungantur PL, MP, & producantur eæ ad m & l, ubi secent planum Eclipticæ; inque Tm demittatur perpendiculum PH. Et quoniam ML parallela est ipsi ST, si ml parallela sit ipsi ML, erit ml in plano Eclipticæ, & contra. Ergo ml, cum sit in plano Eclipticæ, parallela erit ipsi ML, & similia erunt triangula LMP, Lmp. Jam cum MPm sit in plano Orbis, in quo Luna in loco P movebatur, incidet punctum m in lineam Nn per Orbis illius Nodos N, n, ductam. Et quoniam vis qua lineola LM generatur, si tota simul & semel in loco P impressa esset, efficeret ut Luna moveretur in arcu, cujus Chorda esset LP, atque adeò transferret Lunam de plano MPmT in planum LPlT; motus Nodorum à vi illa genitus æqualis erit angulo mTl. Est autem ml ad mP ut ML ad MP, adeoque cum MP ob datum tempus data sit, est ml ut rectangulum ML × mP, id est ut rectangulum IT × mP. Et angulus mTl, si modo angulus Tml rectus sit, est ut ml ÷ Tm, & propterea ut IT × Pm ÷ Tm id est (ob proportionales Tm & mP, TP & PH) ut IT × PH ÷ TP, adeoque ob datam TP, ut IT × PH. Quod si angulus Tml, seu STN obliquus sit, erit angulus mTl adhuc minor, in ratione Sinus anguli STN ad Radium. Est igitur velocitas Nodorum ut IT × PH & Sinus anguli STN conjunctim, sive ut contentum sub sinubus trium angulorum TPI, PTN & STN.

Si anguli illi, Nodis in Quadraturis & Luna in Syzygia existentibus, recti sint, lineola ml abibit in infinitum, & angulus mTl evadet angulo mPl æqualis. Hoc autem in casu, angulus mPl est ad angulum PTM, quem Luna eodem tempore motu suo apparente circa Terram describit ut 1 ad 59,575. Nam angulus mPl æqualis est angulo LPM, id est angulo deflexionis Lunæ à recto tramite, quam præfata vis Solaris 3IT dato illo tempore generare possit; & angulus PTM æqualis est angulo deflexionis Lunæ à recto tramite, quem vis illa, qua Luna in Orbe suo retinetur, eodem tempore generat. Et hæ vires, uti supra diximus, sunt ad invicem ut 1 ad 59,575. Ergo cum motus medius horarius Lunæ (respectu fixarum) sit 32′. 56″. 27″′. 12^iv½, motus horarius Nodi in hoc casu erit 33″. 10″′. 33^iv. 12^v. Aliis autem in casibus motus iste horarius erit ad 33″. 10″′. 33^iv. 12^v. ut contentum sub sinibus angulorum trium TPI, PTN, & STN (seu distantiarum Lunæ à Quadratura, Lunæ à Nodo & Nodi à Sole) ad cubum Radii. Et quoties signum anguli alicujus de affirmativo in negativum, deque negativo in affirmativum mutatur, debebit motus regressivus in progressivum & progressivus in regressivum mutari. Unde fit ut Nodi progrediantur quoties Luna inter Quadraturam alterutram & Nodum Quadraturæ proximum versatur. Aliis in casibus regrediuntur, & per excessum regressus supra progressum, singulis mensibus feruntur in antecedentia.

Corol. 1. Hinc si a dati arcus quam minimi PM terminis P & M ad lineam Quadraturas jungentem Qq demittantur perpendicula PK, Mk, eademque producantur donec secent lineam Nodorum Nn in D & d; erit motus horarius Nodorum ut area MPDd & quadratum lineæ AZ conjunctim. Sunto enim PK, PH & AZ prædicti tres Sinus. Nempe PK Sinus distantiæ Lunæ à Quadratura, PH Sinus distantiæ Lunæ à Nodo, & AZ Sinus distantiæ Nodi à Sole: & erit velocitas Nodi ut contentum PK × PH × AZ. Est autem PT ad PK ut PM ad Kk, adeoque ob datas PT & PM est Kk ipsi PK proportionalis. Est & AT ad PD ut AZ ad PH, & propterea PH rectangulo PD × AZ proportionalis, & conjunctis rationibus, PK × PH est ut contentum Kk × PD × AZ, & PK × PH × AZ ut Kk × PD × AZ qu. id est ut area PDdM, & AZ qu. conjunctim.   Q. E. D.

Corol. 2. In data quavis Nodorum positione, motus horarius mediocris est semissis motus horarii in Syzygiis Lunæ, ideoque est ad 16″. 35″′. 16^iv. 36^v. ut quadratum Sinus distantiæ Nodorum à Syzygiis ad quadratum Radii, sive ut AZ qu. ad AT qu. Nam si Luna uniformi cum motu perambulet semicirculum QAq, summa omnium arearum PDdM, quo tempore Luna pergit à Q ad M, erit area QMdE quæ ad circuli tangentem QE terminatur; & quo tempore Luna attingit punctum n, summa illa erit area tota EQAn quam linea PD describit; dein Luna pergente ab n ad q, linea PD cadet extra circulum, & aream nqe ad circuli tangentem qe terminatam describet; quæ, quoniam Nodi prius regrediebantur, jam verò progrediuntur, subduci debet de area priore, & cum æqualis sit areæ QEN, relinquet semicirculum NQAn. Igitur summa omnium arearum PDdM, quo tempore Luna semicirculum describit, est area semicirculi; & summa omnium quo tempore Luna circulum describit est area circuli totius. At area PDdM, ubi Luna versatur in Syzygiis, est rectangulum sub arcu PM & radio MT; & summa omnium huic æqualium arearum, quo tempore Luna circulum describit, est rectangulum sub circumferentia tota & radio circuli; & hoc rectangulum, cum sit æquale duobus circulis, duplo majus est quàm rectangulum prius. Proinde Nodi, eâ cum velocitate uniformiter continuatâ quam habent in Syzygiis Lunaribus, spatium duplo majus describerent quàm revera describunt; & propterea motus mediocris quocum, si uniformiter continuaretur, spatium à se inæquabili cum motu revera confectum describere possent, est semissis motus quem habent in Syzygiis Lunæ. Unde cum motus orarius maximus, si Nodi in Quadraturis versantur, sit 33″. 10″′. 33^iv. 12^v, motus mediocris horarius in hoc casu erit 16″. 35″′. 16^iv. 36^v. Et cum motus horarius Nodorum semper sit ut AZ qu. & area PDdM conjunctim, & propterea motus horarius Nodorum in Syzygiis Lunæ ut AZ qu. & area PDdM conjunctim, id est (ob datam aream PDdM in Syzygiis descriptam) ut AZ qu. erit etiam motus mediocris ut AZ qu. atque adeo hic motus, ubi Nodi extra Quadraturas versantur, erit ad 16″. 35″′. 16^iv. 36^v. ut AZ qu. ad AT qu. Q. E. D.

Prop. XXXI. Prob. XI.

Invenire motum horarium Nodorum Lunæ in Orbe Elliptico.

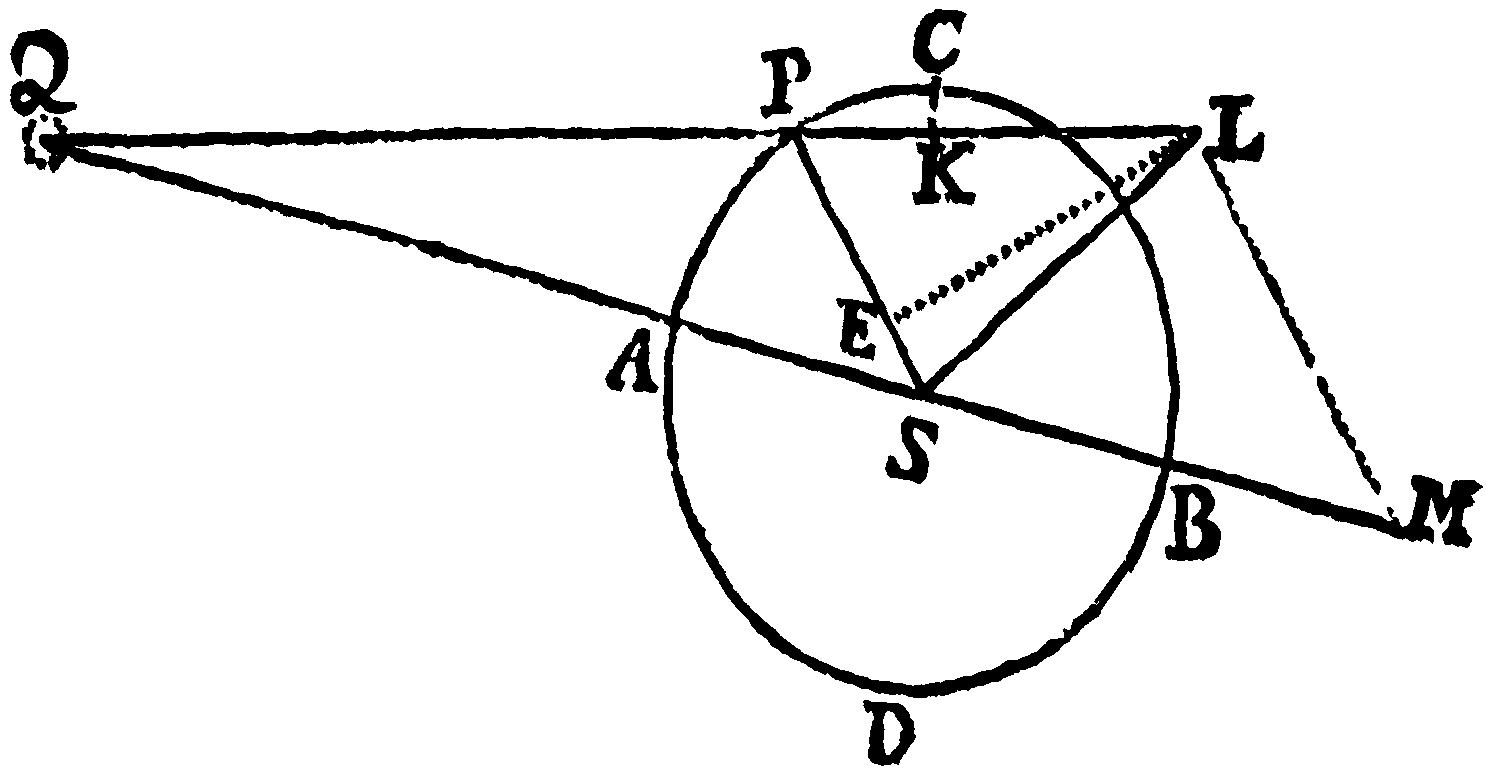
Designet Qpmaq Ellipsim, axe majore Qq, minore ab descriptam, QAq circulum circumscriptum, T Terram in utriusque centro communi, S Solem, p Lunam in Ellipsi moventem, & pm arcum quem data temporis particula quam minima describit, N & n Nodos linea Nn junctos, pK & mk perpendicula in axem Qq demissa & hinc inde producta, donec occurrant circulo in P & M, & lineæ Nodorum in D & d. Et si Luna, radio ad Terram ducto, aream describat tempori proportionalem, erit motus Nodi in Ellipsi ut area pDdm.

Nam si PF tangat circulum in P, & producta occurrat TN in F, & pf tangat Ellipsin in p & producta occurrat eidem TN in f, conveniant autem hæ Tangentes in axe TQ ad Y; & si ML designet spatium quod Luna in circulo revolvens, interea dum describit arcum PM, urgente & impellente vi prædicta 3IT, motu transverso describere posset, & ml designet spatium quod Luna in Ellipsi revolvens eodem tempore, urgente etiam vi 3IT, describere posset; & producantur LP & lp donec occurrant plano Eclipticæ in G & g; & jungantur FG & fg, quarum FG producta secet pf, pg & TQ in c, e & R respectivè, & fg producta secet TQ in r: Quoniam vis 3IT seu 3PK in circulo est ad vim 3IT seu 3pK in Ellipsi, ut PK ad pK, seu AT ad aT; erit spatium ML vi priore genitum, ad spatium ml vi posteriore genitum, ut PK ad pK, id est ob similes figuras PYKp & FYRc, ut FR ad cR. Est autem ML ad FG (ob similia triangula PLM, PGF) ut PL ad PG, hoc est (ob parallelas Lk, PK, GR) ut pl ad pe, id est (ob similia triangula plm, cpe) ut lm ad ce; & inversè ut LM est ad lm, seu FR ad cR, ita est FG ad ce. Et propterea si fg esset ad ce ut fY ad cY, id est ut fr ad cR, (hoc est ut fr ad FR & FR ad cR conjunctim, id est ut fT ad FT & FG ad ce conjunctim,) quoniam ratio FG ad ce utrinque ablata relinquit rationes fg ad FG & fT ad FT, foret fg ad FG ut fT ad FT; propterea quod anguli, quos FG & fg subtenderent ad Terram T, æquarentur inter se. Sed anguli illi (per ea quæ in præcedente Propositione exposuimus) sunt motus Nodorum, quo tempore Luna in circulo arcum PM, in Ellipsi arcum pm percurrit: & propterea motus Nodorum in Circulo & Ellipsi æquarentur inter se. Hæc ita se haberent, si modo fg esset ad ce ut fY ad cY, id est si fg æqualis esset ce × fY ÷ cY. Verum ob similia triangula fgp, cep, est fg ad ce ut fp ad cp; ideoque fg æqualis est ce × fp ÷ cp, & propterea angulus, quem fg revera subtendit, est ad angulum priorem, quem FG subtendit, hoc est motus Nodorum in Ellipsi ad motum Nodorum in Circulo, ut hæc fg seu ce × fp ÷ cp ad priorem fg seu ce × fY ÷ cY, id est ut fp × cY ad cp × fY, seu fp ad fY & cY ad cp; hoc est, si pb ipsi TN parallela occurrat FP in b, ut Fb ad FY & FY ad FP; hoc est ut Fb ad FP seu Dp ad DP, adeoque ut area Dpmd ad aream DPMd. Et propterea, cum area posterior proportionalis sit motui Nodorum in Circulo, erit area prior proportionalis motui Nodorum in Ellipsi.   Q. E. D.

Corol. Igitur cum, in data Nodorum positione, summa omnium arearum pDdm, quo tempore Luna pergit à Quadratura ad locum quemvis m, sit area mpQEd, quæ ad Ellipseos Tangentem QE terminatur; & summa omnium arearum illarum, in revolutione integra, sit area Ellipseos totius: motus mediocris Nodorum in Ellipsi erit ad motum mediocrem Nodorum in circulo, ut Ellipsis ad circulum, id est ut Ta ad TA, seu 68¹¹/₁₂ ad 69¹¹/₁₂. Et propterea, cum motus mediocris horarius Nodorum in circulo sit ad 16″. 35″′. 16^iv. 36^v. ut AZ qu. ad AT qu. si capiatur angulus 16″. 21″′. 2^iv. 36^v. ad angulum 16″. 35″′. 16^iv. 36^v. ut 68¹¹/₁₂ ad 69¹¹/₁₂, erit motus mediocris horarius Nodorum in Ellipsi ad 16″. 21″′. 2^iv. 36^v. ut AZq. ad ATq.; hoc est ut quadratum Sinus distantiæ Nodi à Sole ad quadratum Radii.

Cæterum Luna, radio ad Terram ducto, aream velocius describit in Syzygiis quàm in Quadraturis, & eo nomine tempus in Syzygiis contrahitur, in Quadraturis producitur; & una cum tempore motus Nodorum augetur ac diminuitur. Erat autem momentum areæ in Quadraturis Lunæ ad ejus momentum in Syzygiis ut 10973 ad 11073; & propterea momentum mediocre in Octantibus est ad excessum in Syzygiis, defectumque in Quadraturis, ut numerorum semisumma 11023 ad eorundem semidifferentiam 50. Unde cum tempus Lunæ in singulis Orbis particulis æqualibus sit reciprocè ut ipsius velocitas, erit tempus mediocre in Octantibus ad excessum temporis in Quadrantibus, ac defectum in Syzygiis, ab hac causa oriundum, ut 11023 ad 50 quam proxime. Pergendo autem à Quadraturis ad Syzygias, invenio quod excessus momentorum areæ in locis singulis, supra momentum minimum in Quadraturis, sit ut quadratum Sinus distantiæ Lunæ à Quadrantibus quam proximè; & propterea differentia inter momentum in loco quocunque & momentum mediocre in Octantibus, est ut differentia inter quadratum Sinus distantiæ Lunæ à Quadraturis & quadratum Sinus graduum 45, seu semissem quadrati Radii; & incrementum temporis in locis singulis inter Octantes & Quadraturas, & decrementum ejus inter Octantes & Syzygias est in eadem ratione. Motus autem Nodorum, quo tempore Luna percurrit singulas Orbis particulas æquales, acceleratur vel retardatur in duplicata ratione temporis. Est enim motus iste, dum Luna percurrit PM, (cæteris paribus) ut ML, & ML est in duplicata ratione temporis. Quare motus Nodorum in Syzygiis, eo tempore confectus quo Luna datas Orbis particulas percurrit, diminuitur in duplicata ratione numeri 11073 ad numerum 11023; estque decrementum ad motum reliquum ut 100 ad 10973, ad motum verò totum ut 100 ad 11073 quam proximè. Decrementum autem in locis inter Octantes & Syzygias, & incrementum in locis inter Octantes & Quadraturas, est quam proxime ad hoc decrementum, ut motus totus in locis illis ad motum totum in Syzygiis & differentia inter quadratum Sinus distantiæ Lunæ à Quadratura & semissem quadrati Radii ad semissem quadrati Radii, conjunctim. Unde si Nodi in Quadraturis versentur, & capiantur loca duo æqualiter ab Octante hinc inde distantia, & alia duo à Syzygiâ & Quadraturâ iisdem intervallis distantia, deque decrementis motuum in locis duabus inter Syzygiam & Octantem, subducantur incrementa motuum in locis reliquis duobus, quæ sunt inter Octantem & Quadraturam; decrementum reliquum æquale erit decremento in Syzygia: uti rationem ineunti facilè constabit. Proindeque decrementum mediocre, quod de Nodorum motu mediocri subduci debet, est pars quarta decrementi in Syzygia. Motus totus horarius Nodorum in Syzygiis (ubi Luna radio ad Terram ducto aream tempori proportionalem describere supponebatur) erat 32″. 42″′. 5^iv. 12^v. Et decrementum motus Nodorum, quo tempore Luna jam velocior describit idem spatium, diximus esse ad hunc motum ut 100 ad 11073; adeoque decrementum illud est 17″′. 43^iv. 10^v, cujus pars quarta 4″′. 25^iv. 48^v, motui horario mediocri superius invento 16″. 21″′. 2^iv. 36^v. subducta, relinquit 16″. 16″′. 36^iv. 48^v. motum mediocrem horarium correctum.

Si Nodi versantur extra Quadraturas, & spectentur loca bina à Syzygiis hinc inde æqualiter distantia; summa motuum Nodorum, ubi Luna versatur in his locis, erit ad summam motuum, ubi Luna in iisdem locis & Nodi in Quadraturis versantur, ut AZ qu. ad AT qu. Et decrementa motuum, à causis jam expositis oriunda, erunt ad invicem ut ipsi motus, adeoque motus reliqui erunt ad invicem ut AZ qu. ad AT qu. & motus mediocres ut motus reliqui. Est itaque motus mediocris horarius correctus, in dato quocunque Nodorum situ, ad 16″. 16″′. 36^iv. 48^v. ut AZ qu. ad AT qu.; id est ut quadratum Sinus distantiæ Nodorum à Syzygiis ad quadratum Radii.

Prop. XXXII. Prob. XII.

Invenire motum medium Nodorum Lunæ.

Motus medius annuus est summa motuum omnium horariorum mediocrium in anno. Concipe Nodum versari in N, & singulis horis completis retrahi in locum suum priorem, ut non obstante motu suo proprio, datum semper servet situm ad Stellas Fixas. Interea verò Solem S, per motum Terræ, progredi à Nodo, & cursum annuum apparentem uniformiter complere. Sit autem Aa arcus datus quam minimus, quem recta TS ad Solem semper ducta, intersectione sua & circuli NAn, dato tempore quam minimo describit: & motus horarius mediocris (per jam ostensa) erit ut AZq. id est (ob proportionales AZ, ZY) ut rectangulum sub AZ & ZY, hoc est ut area AZYa. Et summa omnium horariorum motuum mediocrium ab initio, ut summa omnium arearum aYZA, id est ut area NAZ. Est autem maxima AZYa æqualis rectangulo sub arcu Aa & radio circuli; & propterea summa omnium rectangulorum in circulo toto ad summam totidem maximorum, ut area circuli totius ad rectangulum sub circumferentia tota & radio; id est ut 1 ad 2. Motus autem horarius, rectangulo maximo respondens, erat 16″. 16″′. 36^iv. 48^v. Et hic motus, anno toto sidereo dierum 365. 6 hor. 9 min. fit 39 gr. 38′. 5″. 39″′. Ideoque hujus dimidium 19 gr. 49′. 2″. 49″′½ est motus medius Nodorum circulo toti respondens. Et motus Nodorum, quo tempore Sol pergit ab N ad A, est ad 19 gr. 49′. 2″. 49″′½ ut area NAZ ad circulum totum.

Hæc ita se habent, ex Hypothesi quod Nodus horis singulis in locum priorem retrahitur, sic ut Sol anno toto completo ad Nodum eundem redeat à quo sub initio digressus fuerat. Verum per motum Nodi fit ut Sol citius ad Nodum revertatur, & computanda jam est abbreviatio temporis. Cum Sol anno toto conficiat 360 gradus, & Nodus motu maximo eodem tempore conficeret 39 gr. 38′. 5″. 39″′. seu 39,6349 gradus; & motus mediocris Nodi in loco quovis N sit ad ipsius motum mediocrem in Quadraturis suis, ut AZq. ad ATq. erit motus Solis ad motum Nodi in N, ut 360 ATq. ad 39,6349 AZq.; id est ut 9,0829032 ATq. ad AZq. Unde si circuli totius circumferentia NAn dividatur in particulas æquales Aa, tempus quo Sol percurrat particulam Aa, si circulus quiesceret, erit ad tempus quo percurrit eandem particulam, si circulus una cum Nodis circa centrum T revolvatur, reciprocè ut 9,0829032 ATq. ad 9,0829032 ATq. + AZq. Nam tempus est reciprocè ut velocitas qua particula percurritur, & hæc velocitas est summa velocitatum Solis & Nodi. Igitur si tempus, quo Sol absque motu Nodi percurreret arcum NA, exponatur per Sectorem NTA, & particula temporis quo percurreret arcum quam minimum Aa, exponatur per Sectoris particulam ATa; & (perpendiculo aY in Nn demisso) si in AZ capiatur dZ, ejus longitudinis ut sit rectangulum dZ in ZY ad Sectoris particulam ATa ut AZq. ad 9,0829032 ATq. + AZq. id est ut sit dZ ad ½AZ ut ATq. ad 9,0829032 ATq. + AZq.; rectangulum dZ in ZY designabit decrementum temporis ex motu Nodi oriundum, tempore toto quo arcus Aa percurritur. Et si punctum d tangit curvam NdGn, area curvilinea NdZ erit decrementum totum, quo tempore arcus totus NA percurritur; & propterea excessus Sectoris NAT supra aream NdZ erit tempus illud totum. Et quoniam motus Nodi tempore minore minor est in ratione temporis, debebit etiam area AaYZ diminui in eadem ratione. Id quod fiet si capiatur in AZ longitudo eZ, quæ sit ad longitudinem AZ ut AZq. ad 9,08299032 ATq. + AZq. Sic enim rectangulum eZ in ZY erit ad aream AZYa ut decrementum temporis, quo arcus Aa percurritur, ad tempus totum, quo percurreretur si Nodus quiesceret: Et propterea rectangulum illud respondebit decremento motus Nodi. Et si punctum e tangat curvam NeFn, area tota NeZ, quæ summa est omnium decrementorum, respondebit decremento toti, quo tempore arcus AN percurritur; & area reliqua NAe respondebit motui reliquo, qui verus est Nodi motus quo tempore arcus totus NA, per Solis & Nodi conjunctos motus, percurritur. Jam verò si circuli radius AT ponatur 1, erit area semicirculi 1,570796; & area figuræ NeFnT, per methodum Serierum infinitarum quæsita, prodibit 0,1188478. Motus autem qui respondet circulo toti erat 19 gr. 49′. 2″. 49″′½; & propterea motus, qui figuræ NeFnT duplicatæ respondet, est 1 gr. 29′. 57″. 51″′½. Qui de motu priore subductus relinquit 18 gr. 19′. 4″. 58″′. motum totum Nodi inter sui ipsius Conjunctiones cum Sole; & hic motus de Solis motu annuo graduum 360 subductus, relinquit 341 gr. 40′. 55″. 2″′. motum Solis inter easdem Conjunctiones. Iste autem motus est ad motum annuum 360 gr. ut Nodi motus jam inventus 18 gr. 19′. 4″. 58″′. ad ipsius motum annuum, qui propterea erit 19 gr. 18′. 0″. 22″′. Hic est motus medius Nodorum in anno sidereo. Idem per Tabulas Astronomicas est 19 gr. 20′. 31″. 1″′. Differentia minor est parte quadringentesima motus totius, & ab Orbis Lunaris Excentricitate & Inclinatione ad planum Eclipticæ oriri videtur. Per Excentricitatem Orbis motus Nodorum nimis acceleratur, & per ejus Inclinationem vicissim retardatur aliquantulum, & ad justam velocitatem reducitur.

Prop. XXXIII. Prob. XIII.

Invenire motum verum Nodorum Lunæ.

In tempore quod est ut area NTA - NdZ, (in Fig. præced.) motus iste est ut area NAeN, & inde datur. Verum ob nimiam calculi difficultatem, præstat sequentem Problematis constructionem adhibere. Centro C, intervallo quovis CD, describatur circulus BEFD. Producatur DC ad A, ut sit AB ad AC ut motus medius ad semissem motus veri mediocris, ubi Nodi sunt in Quadraturis: (id est ut 19 gr. 18′. 0″. 22″′. ad 19 gr. 49′. 2″. 49″′½, atque adeo BC ad AC ut motuum differentia 0 gr. 31′. 2″. 27″′½, ad motum posteriorem 19 gr. 49′. 2″. 49″′½, hoc est, ut 1. ad 38⅓) dein per punctum D ducatur infinita Gg, quæ tangat circulum in D; & si capiatur angulus BCE vel BCF æqualis semissi distantiæ Solis à loco Nodi, per motum medium invento; & agatur AE vel AF secans perpendiculum DG in G; & capiatur angulus qui sit ad motum Nodi inter ipsius Syzygias (id est ad 9 gr. 10′. 40″.) ut tangens DG ad circuli BED circumferentiam totam, atque angulus iste ad motum medium Nodorum addatur; habebitur eorum motus verus. Nam motus verus sic inventus congruet quam proximè cum motu vero qui prodit exponendo tempus per aream NTA - NdZ, & motum Nodi per aream NAeN; ut rem perpendenti constabit. Hæc est æquatio annua motus Nodorum. Est & æquatio menstrua, sed quæ ad inventionem Latitudinis Lunæ minimè necessaria est. Nam cum Variatio inclinationis Orbis Lunaris ad planum Eclipticæ duplici inæqualitati obnoxia sit, alteri annuæ, alteri autem menstruæ; hujus menstrua inæqualitas & æquatio menstrua Nodorum ita se mutuò contemperant & corrigunt, ut ambæ in determinanda Latitudine Lunæ negligi possint.

Corol. Ex hac & præcedente Propositione liquet quod Nodi in Syzygiis suis quiescunt, in Quadraturis autem regrediuntur motu horario 16″. 18″′. 41^iv½. Et quod æquatio motus Nodorum in Octantibus sit 1 gr. 30′. Quæ omnia cum Phænomenis cœlestibus probè quadrant.

Prop. XXXIV. Prob. XIV.

Invenire Variationem horariam inclinationis Orbis Lunaris ad planum Eclipticæ.

Designent A & a Syzygias; Q & q Quadraturas; N & n Nodos; P locum Lunæ in Orbe suo; p vestigium loci illius in plano Eclipticæ, & mTl motum momentaneum Nodorum ut supra. Et si ad lineam Tm demittatur perpendiculum PG, jungatur pG, & producatur ea donec occurrat Tl in g, & jungatur etiam Pg: erit angulus PGp inclinatio orbis Lunaris ad planum Eclipticæ, ubi Luna versatur in P; & angulus Pgp inclinatio ejusdem post momentum temporis completum, adeoque angulus GPg Variatio momentanea inclinationis. Est autem hic angulus GPg ad angulum GTg ut TG ad PG & Pp ad PG conjunctim. Et propterea si pro momento temporis substituatur hora; cum angulus GTg (per Prop. XXX.) sit ad angulum 33″. 10″′. 33^iv. ut IT × PG × AZ ad AT cub. erit angulus GPg (seu inclinationis horaria Variatio) ad angulum 33″. 10″′. 33^iv. ut IT × AZ × TG × Pp ÷ PG ad AT cub.   Q. E. I.

Hæc ita se habent ex Hypothesi quod Luna in Orbe circulari uniformiter gyratur. Quod si orbis ille Ellipticus sit, motus mediocris Nodorum minuetur in ratione axis minoris ad axem majorem; uti supra expositum est. Et in eadem ratione minuetur etiam Sinus IT. Inclinationis autem Variatio tantum augebitur per decrementum Sinus IT, quantum diminuitur per decrementum motus Nodorum; & propterea idem manebit atque prius.

Corol. 1. Si ad Nn erigatur perpendiculum TF, sitque pM motus horarius Lunæ in plano Eclipticæ; & perpendicula pK, Mk in QT demissa & utrinque producta occurrant TF in H & h: erit Kk ad Mp ut pK seu IT ad AT, & TZ ad AT ut TG ad Hp; ideoque IT × TG æquale Kk × Hp × TZ ÷ Mp, hoc est æquale areæ HpMh ductæ in rationem TZ ÷ Mp: & propterea inclinationis Variatio horaria ad 33″. 10″′. 33^iv. ut HpMh ducta in AZ × {TZ ÷ Mp} × {Pp ÷ PG} ad AT cub.

Corol. 2. Ideoque si Terra & Nodi singulis horis completis retraherentur à locis suis novis, & in loca priora in instanti semper reducerentur, ut situs eorum, per mensem integrum periodicum, datus maneret; tota Inclinationis Variatio tempore mensis illius foret ad 33″. 10″′. 33^iv, ut aggregatum omnium arearum HpMh, in revolutione puncti p generatarum, & sub signis propriis + & - conjunctarum, ductum in AZ × TZ × Pp ÷ PG, ad Mp × AT cub. id est ut circulus totus QAqa ductus in AZ × TZ × Pp ÷ PG ad Mp × AT cub. hoc est ut circumferentia QAqa ducta in AZ × TZ × Pp ÷ PG ad 2MP × AT quad.

Corol. 3. Proinde in dato Nodorum situ, Variatio mediocris horaria, ex quâ per mensem uniformiter continuatâ Variatio illa menstrua generari posset, est ad 33″. 10″′. 33^iv. ut AZ × TZ × Pp ÷ PG ad 2ATq. id est (cum Pp sit ad PG ut Sinus Inclinationis prædictæ ad Radium, & AZ × TZ ÷ AT sit ad ½AT ut sinus duplicati anguli ATn ad Radium) ut inclinationis ejusdem Sinus ductus in Sinum duplicatæ distantiæ Nodorum à Sole, ad quadruplum quadratum Radii.

Corol. 4. Quoniam inclinationis horaria Variatio, ubi Nodi in Quadraturis versantur, est (per Propositionem superiorem) ad angulum 33″. 10″′. 33^iv. ut IT × AZ × TG × Pp ÷ PG ad AT cub. id est ut {IT × TG ÷ AT} × {Pp ÷ PG} ad AT; hoc est ut Sinus duplicatæ distantiæ Lunæ à Quadraturis ductus in Pp ÷ PG ad radium duplicatum: summa omnium Variationum horariarum, quo tempore Luna in hoc situ Nodorum transit à Quadratura ad Syzygiam, (id est spatio horarum 177¹/₆,) erit ad summam totidem angulorum 33″. 10″′. 33^iv. seu 5878″½, ut summa omnium sinuum duplicatæ distantiæ Lunæ à Quadraturis ducta in Pp ÷ PG ad summam totidem diametrorum; hoc est ut diameter ducta in Pp ÷ PG, ad circumferentiam; id est si inclinatio sit 5 gr. 2′, ut 7 × ⁸⁷⁶/₁₀₀₀₀ ad 22, seu 279 ad 10000. Proindeque Variatio tota, ex summa omnium horariarum Variationum tempore prædicto conflata, est 164″, seu 2′. 44″.

Prop. XXXV. Prob. XV.

Dato tempore invenire Inclinationem Orbis Lunaris ad planum Eclipticæ.

Sit AD Sinus inclinationis maximæ, & AB Sinus Inclinationis minimæ. Bisecetur BD in C, & centro C, intervallo BC, describatur Circulus BGD. In AC capiatur CE in ea ratione ad EB quam EB habet ad 2BA: Et si dato tempore constituatur angulus AEG æqualis duplicatæ distantiæ Nodorum à Quadraturis, & ad AD demittatur perpendiculum GH: erit AH Sinus inclinationis quæsitæ.

Nam GEq. æquale est GHq. + HEq. = BHD + HEq. = HBD + HEq. - BHq. = HBD + BEq. - 2BH × BE = BEq. + 2EC × BH = 2EC × AB + 2EC × BH = 2EC × AH. Ideoque cum 2EC detur, est GEq. ut AH. Designet jam AEg distantiam Nodorum à Quadraturis post datum aliquod momentum temporis completum, & arcus Gg, ob datum angulum GEg, erit ut distantia GE. Est autem Hh ad Gg ut GH ad GC, & propterea Hh est ut contentum GH × Gg seu GH × GE; id est ut {GH ÷ GE} × GE qu. seu {GH ÷ GE} × AH, id est ut AH & sinus anguli AEG conjunctim. Igitur si AH in casu aliquo sit Sinus inclinationis, augebitur ea iisdem incrementis cum sinu inclinationis, per Corol. 3. Propositionis superioris, & propterea sinui illi æqualis semper manebit. Sed AH ubi punctum G incidit in punctum alterutrum B vel D huic Sinui æqualis est, & propterea eidem semper æqualis manet.   Q. E. D.

In hac demonstratione supposui angulum BEG, qui distantia est Nodorum à Quadraturis, uniformiter augeri. Nam omnes inæqualitatum minutias expendere non vacat. Concipe jam angulum BEG rectum esse, & Gg esse augmentum horarium distantiæ Nodorum & Solis ab invicem; & inclinationis Variatio horaria (per Corol. 3. Prop. novissimæ) erit ad 33″. 10″′. 33^iv. ut contentum sub inclinationis Sinu AH & Sinu anguli recti BEG, qui est duplicata distantia Nodorum à Sole, ad quadruplum quadratum Radii; id est ut mediocris inclinationis Sinus AH ad radium quadruplicatum; hoc est (cum inclinatio illa mediocris sit quasi 5 gr. 8′½.) ut ejus Sinus 896 ad radium quadruplicatum 40000, sive ut 224 ad 10000. Est autem Variatio tota, Sinuum differentiæ BD respondens, ad variationem illam horariam ut diameter BD ad arcum Gg; id est ut diameter BD ad semicircumferentiam BGD & tempus horarum 2080, quo Nodus pergit à Quadraturis ad Syzygias, ad horam unam conjunctim; hoc est ut 7 ad 11 & 2080 ad 1. Quare si rationes omnes conjungantur, fiet Variatio tota BD ad 33″. 10″′. 33^iv. ut 224 × 7 × 2080 ad 110000, id est ut 2965 ad 100, & inde Variatio illa BD prodibit 16′. 24″.

Hæc est inclinationis Variatio maxima quatenus locus Lunæ in Orbe suo non consideratur. Nam inclinatio, si Nodi in Syzygiis versantur, nil mutatur ex vario situ Lunæ. At si Nodi in Quadraturis consistunt, inclinatio major est ubi Luna versatur in Syzygiis, quàm ubi ea versatur in Quadraturis, excessu 2′. 44″; uti in Propositionis superioris Corollario quarto indicavimus. Et hujus excessus dimidio 1′. 22″ Variatio tota mediocris BD in Quadraturis Lunaribus diminuta fit 15′. 2″, in ipsius autem Syzygiis aucta fit 17′. 46″. Si Luna igitur in Syzygiis constituatur, Variatio tota, in transitu Nodorum à Quadraturis ad Syzygias, erit 17′. 46″. adeoque si Inclinatio, ubi Nodi in Syzygiis versantur, sit 5 gr. 17′. 46″. eadem, ubi Nodi sunt in Quadraturis, & Luna in Syzygiis, erit 5 gr. Atque hæc ita se habere confirmatur ex Observationibus. Nam statuunt Astronomi Inclinationem Orbis Lunaris ad planum Eclipticæ, ubi Nodi sunt in Quadraturis & Luna in oppositione Solis, esse quasi 5 gr. Ubi verò Nodi sunt in Syzygiis, eandem docent esse 5 gr. 17′½ vel 5 gr. 18′.

Si jam desideretur Orbis Inclinatio illa, ubi Luna in Syzygiis & Nodi ubivis versantur; fiat AB ad AD ut Sinus 5 gr. ad Sinum 5 gr. 17′. 46″, & capiatur angulus AEG æqualis duplicatæ distantiæ Nodorum à Quadraturis; & erit AH Sinus Inclinationis quæsitæ. Huic Orbis Inclinationi æqualis est ejusdem Inclinatio, ubi Luna distat 90 gr. à Nodis. Aliis in Lunæ locis inæqualitas menstrua, quam Inclinationis variatio admittit, in calculo Latitudinis Lunæ compensatur & quodammodo tollitur per inæqualitatem menstruam motus Nodorum, (ut supra diximus) adeoque in calculo Latitudinis illius negligi potest.

Scholium.

Hactenus de motibus Lunæ quatenus Excentricitas Orbis non consideratur. Similibus computationibus inveni, quod Apogæum ubi in Conjunctione vel Oppositione Solis versatur, progreditur singulis diebus 23′ respectu Fixarum; ubi verò in Quadraturis est, regreditur singulis diebus 16⅓ circiter: quodque ipsius motus medius annuus sit quasi 40 gr. Per Tabulas Astronomicas à Cl. Flamstedio ad Hypothesin Horroxii accommodatas, Apogæum in ipsius Syzygiis progreditur cum motu diurno 24′. 28″, in Quadraturis autem regreditur cum motu diurno 20′. 12″, & motu medio annuo 40 gr. 41′ fertur in consequentia. Quod differentia inter motum diurnum progressivum Apogæi in ipsius Syzygiis, & motum diurnum regressivum in ipsius Quadraturis, per Tabulas sit 4′. 16″, per computationem verò nostram 6′⅔, vitio Tabularum tribuendum esse suspicamur. Sed neque computationem nostram satis accuratam esse putamus. Nam rationem quandam ineundo prodiere Apogæi motus diurnus progressivus in ipsius Syzygiis, & motus diurnus regressivus in ipsius Quadraturis, paulo majores. Computationes autem, ut nimis perplexas & approximationibus impeditas, neque satis accuratas, apponere non lubet.

Prop. XXXVI. Prob. XVI.

Invenire vim Solis ad Mare movendum.

Solis vis ML seu PS, in Quadraturis Lunaribus, ad perturbandos motus Lunares, erat (per Prop. XXV. hujus) ad vim gravitatis apud nos ut 1 ad 638092,6. Et vis SM - LM seu 2PK in Syzygiis Lunaribus est duplo major. Hæ autem vires, si descendatur ad superficiem Terræ, diminuuntur in ratione distantiarum à centro Terræ, id est in ratione 60½ ad 1; adeoque vis prior in superficie Terræ est ad vim gravitatis ut 1 ad 38604600. Hac vi Mare deprimitur in locis quæ 90 gr. distant à Sole. Vi alterâ quæ duplo major est Mare elevatur, & sub Sole & in regione Soli opposita. Summa virium est ad vim gravitatis ut 1 ad 12868200. Et quoniam vis eadem eundem ciet motum, sive ea deprimat Aquam in regionibus quæ 90 gr. distant à Sole, sive elevet eandem in regionibus sub Sole & Soli oppositis, hæc summa erit tota Solis vis ad Mare agitandum; & eundem habebit effectum ac si tota in regionibus sub Sole & Soli oppositis mare elevaret, in regionibus autem quæ 90 gr. distant à Sole nil ageret.

Corol. Hinc cum vis centrifuga partium Terræ à diurno Terræ motu oriunda, quæ est ad vim gravitatis ut 1 ad 291, efficiat ut altitudo Aquæ sub Æquatore superet ejus altitudinem sub polis mensura pedum Parisiensium 85200, vis Solaris, de qua egimus, cum sit ad vim gravitatis ut 1 ad 12868200, atque adeo ad vim illam centrifugam ut 291 ad 12868200 seu 1 ad 44221, efficiet ut altitudo aquæ in regionibus sub Sole & Soli oppositis superet altitudinem ejus in locis quæ 90 gradibus distant à Sole, mensura tantum pedis unius Parisiensis & digitorum undecim. Est enim hæc mensura ad mensuram pedum 85200 ut 1 ad 44221.

Prop. XXXVII. Prob. XVII.

Invenire vim Lunæ ad Mare movendum.

Vis Lunæ ad mare movendum colligenda est ex ejus proportione ad vim Solis, & hæc proportio colligenda est ex proportione motuum maris, qui ab his viribus oriuntur. Ante ostium fluvii Avonæ, ad lapidem tertium infra Bristoliam, tempore verno & autumnali totus aquæ ascensus in Conjunctione & Oppositione Luminarium (observante Samuele Sturmio) est pedum plus minus 45, in Quadraturis autem est pedum tantum 25: Altitudo prior ex summa virium, posterior ex earundem differentia oritur. Solis igitur & Lunæ in Æquatore versantium & mediocriter à Terra distantium, sunto vires S & L. Et quoniam Luna in Quadraturis, tempore verno & autumnali extra Æquatorem in declinatione graduum plus minus 23½ versatur, & Luminaris ab Æquatore declinantis vis ad mare movendum minor sit, idque (quantum sentio) in duplicata ratione Sinus complementi declinationis quam proximè, vis Lunæ in Quadraturis, (cum sinus ille sit ad radium ut 91706 ad 100000) erit ⁸⁴¹/₁₀₀₀ L, & summa virium in Syzygiis erit L + S, ac differentia in Quadraturis ⁸⁴¹/₁₀₀₀ L - S, adeoque L + S erit ad ⁸⁴¹/₁₀₀₀ L - S ut 45 ad 25 seu 9 ad 5, & inde 5L + 5S æqualis erit ⁷⁵⁶⁹/₁₀₀₀ L - 9S, & 14S æqualis ²⁵⁶⁹/₁₀₀₀ L, & propterea L ad S ut 14000 ad 2569 seu 5⁷/₁₅ ad 1. In Portu Plymuthi æstus maris (ex observatione Samuelis Colepressi) ad pedes plus minus sexdecim, altitudine mediocri attollitur, ac tempore verno & autumnali altitudo æstus in Syzygiis Lunæ superare potest altitudinem ejus in Quadraturis pedibus septem vel octo. Si excessus mediocris his temporibus sit pedum septem cum dimidio; æstus in Syzygiis ascendet ad pedes 19¾, in Quadraturis ad pedes 12¼, & sic L + S erit ad ⁸⁴¹/₁₀₀₀ L - S ut 19¾ ad 12¼, & inde L ad S ut 734 ad 100 seu 7⅓ ad 1. Est igitur vis Lunæ ad vim Solis per computationem priorem ut 5⁷/₁₅ ad 1, per posteriorem ut 7⅓ ad 1. Donec aliquid certius ex Observationibus accuratius institutis constiterit, usurpabimus proportionem mediocrem 6⅓ ad 1. Unde cum vis Solis sit ad vim gravitatis ut 1 ad 12868200, vis Lunæ erit ad vim gravitatis ut 1 ad 2031821.

Corol. 1. Igitur cum aqua vi Solis agitata ad altitudinem pedis unius & undecim digitorum ascendat, eadem vi Lunæ ascendet ad altitudinem pedum duodecim. Tanta autem vis ad omnes maris motus excitandos abunde sufficit, & quantitati motuum probe respondet. Nam in maribus quæ ab Oriente in Occidentem latè patent, uti in Mari Pacifico, & Maris Atlantici & Æthiopici partibus extra Tropicos, aqua attolli solet ad altitudinem pedum sex, novem duodecim vel quindecim. In mari autem Pacifico, quod profundius est & latius patet, æstus dicuntur esse majores quàm in Atlantico & Æthiopico. Etenim ut plenus sit æstus, latitudo Maris ab Oriente in Occidentem non minor esse debet quàm graduum nonaginta. In Mari Æthiopico, ascensus aquæ intra Tropicos minor est quàm in Zonis temperatis, propter angustiam Maris inter Africam & Australem partem Americæ. In medio Mari aqua nequit ascendere nisi ad littus utrumque & orientale & occidentale simul descendat: cum tamen vicibus alternis ad littora illa in Maribus nostris angustis descendere debeat. Ea de causa fluxus & refluxus in Insulis, quæ à littoribus longissimè absunt, perexiguus esset solet. In Portubus quibusdam, ubi aqua cum impetu magno per loca vadosa, ad Sinus alternis vicibus implendos & evacuandos, influere & effluere cogitur, fluxus & refluxus sunt solito majores, uti ad Plymuthum & pontem Chepstowæ in Anglia; ad montes S. Michaelis & urbem Abrincatuorum (vulgo Auranches) in Normania; ad Cambaiam & Pegu in India orientali. His in locis mare, magna cum velocitate accedendo & recedendo, littora nunc inundat nunc arida relinquit ad multa Milliaria. Neque impetus influendi & remeandi prius frangi potest, quam aqua attollitur vel deprimitur ad pedes 30, 40 vel 50 & amplius. Et par est ratio fretorum oblongorum & vadosorum, uti Magellanici & ejus quo Anglia circundatur. Æstus in hujusmodi portubus & fretis per impetum cursus & recursus supra modum augetur. Ad littora verò quæ descensu præcipiti ad mare profundum & apertum spectant, ubi aqua sine impetu effluendi & remeandi attolli & subsidere potest, magnitudo æstus respondet viribus Solis & Lunæ.

Corol. 2. Cum vis Lunæ ad mare movendum sit ad vim gravitatis ut 1 ad 2031821, perspicuum est quod vis illa sit longè minor quàm quæ vel in experimentis Pendulorum, vel in Staticis aut Hydrostaticis quibuscunque sentiri possit. In æstu solo marino hæc vis sensibilem edit effectum.

Corol. 3. Quoniam vis Lunæ ad mare movendum est ad Solis vim consimilem ut 6⅓ ad 1, & vires illæ sunt ut densitates corporum Lunæ & Solis & cubi diametrorum apparentium conjunctim; erit densitas Lunæ ad densitatem Solis ut 6⅓ ad 1 directè & cubus diametri Solis ad cubum diametri Lunæ inversè, id est (cum diametri mediocres apparentes Solis & Lunæ sint 31′. 27″. & 32′. 12″.) ut 34 ad 5. Densitas autem Solis erat ad densitatem Terræ ut 100 ad 387, & propterea densitas Lunæ est ad densitatem Terræ ut 600 ad 387, seu 9 ad 5 quam proximè. Est igitur corpus Lunæ densius & magis terrestre quàm Terra nostra.

Corol. 4. Unde cum vera diameter Lunæ sit ad veram diametrum Terræ ut 1 ad 3,6½, erit massa Lunæ ad massam Terræ ut 1 ad 26 quam proximè.

Corol. 5. Et gravitas acceleratrix in superficie Lunæ, erit quasi duplo minor quàm gravitas acceleratrix in superficie Terræ.

Prop. XXXVIII. Prob. XVIII.

Invenire figuram corporis Lunæ.

Si corpus Lunare fluidum esset ad instar maris nostri, vis Terræ ad fluidum illud in partibus & citimis & ultimis elevandum, esset ad vim Lunæ, qua mare nostrum in partibus & sub Luna & Lunæ oppositis attollitur, ut gravitas acceleratrix Lunæ in Terram ad gravitatem acceleratricem Terræ in Lunam & diameter Lunæ ad diametrum Terræ conjunctim; id est ut 26 ad 1 & 5 ad 18 conjunctim seu 65 ad 9. Unde cum mare nostrum vi Lunæ attollatur ad pedes duodecim, fluidum Lunare vi Terræ attolli deberet ad pedes fere nonaginta. Eaque de causa figura Lunæ Sphærois esset, cujus maxima diameter producta transiret per centrum Terræ, & superaret diametros perpendiculares excessu pedum 180. Talem igitur figuram Luna affectat, eamque sub initio induere debuit.   Q. E. I.

Corol. Inde verò fit ut eadem semper Lunæ facies in Terram obvertatur. In alio enim situ corpus Lunare quiescere non potest, sed ad hunc situm oscillando semper redibit. Attamen oscillationes ob parvitatem virium agitantium essent longè tardissimæ: adeò ut facies illa, quæ Terram semper respicere deberet, possit alterum orbis Lunaris umbilicum, ob rationem superius allatam respicere, neque statim abinde retrahi & in Terram converti.

Lemma I.