Analysis Of Diffraction Pattern Due To Single Slit
Analysis of Diffraction pattern due to single slit: The intensity on the screen for diffraction due to single slit is
where 
. The intensity will be minimum (or zero) when 
or 
m=1,2,...................................... or 
If slit is far from the screen, 
is small such that 
where y is distance of point P from center point P0
and D is distance between slit and screen.
Thus knowing m(order of minima), 
, D and y (separation of m'th minima from principal maxima ) the slit width 'd' can be determined. Now, let us see, when we will observe maxima in diffraction pattern. At the center of screen, the path traveled by the secondary waves originating from one point of slit is same as that traveled by another wave on the opposite side of center of slit at the same distance and hence path difference is zero, ie all the waves meet in phase thus we observe a maxima at this point. This can also be seen mathematically for the intensity distribution equation for point 
,
and 
(for small 
, the series expansion of 
will contain only first term ). Thus the intensity at the center will be
Now we will determine the position of the maxima.
or 
for 
corresponds to minima as discussed earlier. The second condition : 
gives the position of maxima. Solution of transcendental equation can be determined graphically, where two functions 
and 
are plotted against (). The point where these two curves intersects, satisfies 
and these values of 
corresponds to secondary maxima in the diffraction pattern. The corresponding values of 
.This clearly shows that the secondary maximas are not exactly midway between the two minimas but are slightly displaced towards the principle maxima. The intensity at the mid way between two minima is 
where n=1,2,3..... and is slightly less than the intensity at the secondary maxima. The intensity of the first secondary maxima is 
times the intensity of principal maxima.
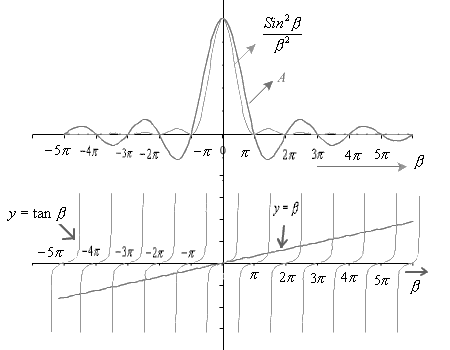fig..(1)
Width of central (principal) maxima The first minima in single slit diffraction pattern occurs for 
. The width of central maxima at a distance D from the slit is thus given by 
, where 
is the distance between the position of peak in central maxima and first minima.
Now for equation
Width of central maxima 
This is the extent to which the light is distributed before diminishing first time. For a given D, ( 
). 2y1 varies as 
. Further for a given 
, y is small if 'd' is large and vice versa. Also if 'd' is fixed, y is small if is small.