Intensity Distribution In Diffraction Pattern By Grating
or, 
more generally,
, p=1,2,............. N-1
= 
(minima)
Thus we see that between two principal consecutive pricipal maxima (say corresponding to 
(central maxima) and 
(first order principal maxima), there are a total 
minima (zero intensity point) appear.
Secondary Maxima(fig..(1)) We have seen that between two adjacent principal maxima, there are 
points where intensity goes to zero. This implies that between two adjacent principal maxima there are at least N-2 points for which intensity goes to a maximum value. These are called secondary maximum and their intensity is not same but falls off as we move away from the principal maxima. Similar to single slit diffraction, these secondary maxima are not equally spaced and are shifted slightly towards the nearest principal maxima.
The intensity of principal maxima and secondary maxima depends on number of slits. When N is large , principal maxima become more intense and narrow and secondary maxima almost disappear .fig..(1), fig..(2)
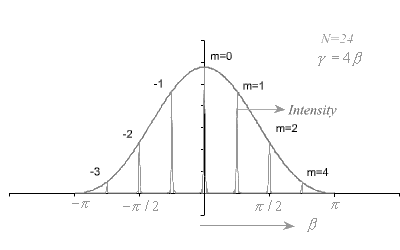fig..(2).
Formation of spectra by Grating Let us now see, what happens if white light (comprising many wavelength) falls on a grating. The resultant intensity distribution on the screen will be due to all the wavelengths. The conditions for central principal maxima 
will be satisfied by all the wavelengths simultaneously and hence a white slit will appear at the centers. However, the other principal maxima for these wavelengths will occur for different values of 
such that 
(order of principal maxima) thus for smaller wavelengths, principal maxima will occur at smaller value and for larger wavelengths, corresponding will be more. The angular separation (20m) between the same order principal maxima on both side of central maxima can thus be used to determine the wavelength of spectral lines in the source.given below (fig..(3),(4),(5) grating
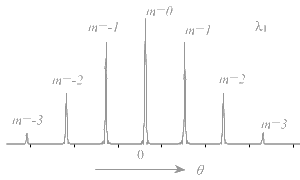fig......(3)
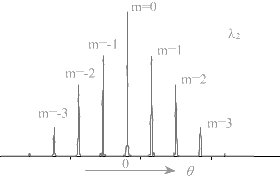fig..(4)
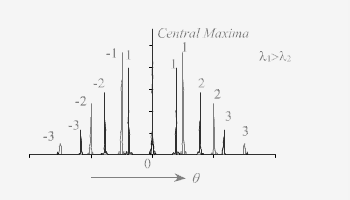fig...(5)