Resolving Power Of Image Forming Systems: Telescope And Microscope
Resolving power of image forming systems: Telescope and Microscope: So far we discussed the diffraction pattern due to apertures which were extending in one dimension only. To calculate the resultant amplitude at a point on screen, we had to perform the integration along one direction only. However, in any image forming system, be it our eye, camera lens, telescope or microscope, light enters through a circular aperture followed by a lens which forms the image on the screen. The image of a distant point source is therefore not a point, but a sort of diffraction pattern. In this case, to calculate the resultant intensity distribution we have to perform a double integral for calculating resultant amplitude, which is quite complex.
However, in this case, we can intutively feel that the diffraction pattern will be in the form of central circular disk surrounded by dark and bright circles. The condition of minima is given by 
, where D is the diameter of the aperture and 
is angular separation of mth order minima from the center. However, in this case m is not an integer as it was for single slit diffraction. Airy showed that the condition for first order minima (first dark circle) is 
.
Telescope When we use a telescope to image two stars, we can determine their angular separation in space. However, whether this resolution is possible, will be determined by the resolving power of telescope. We have seen earlier that two sources can be well resolved if their angular separation 
is such that the central maxima of one falls on the first minima of other (in other words 
)
The condition is equivalent to saying 
.
For small 
(where 
is in radian) Thus if the diameter of lens is large, we can resolve the stars which are nearby. One may argue here that in a telescope, we see the image formed by eye piece and by increasing the power of eye piece we could be able to see the object more clearly. However important point to remember here is that eye piece forms the image, taking image formed by objective lens as object. Thus the features, which are not present in primary image, will not be seen by eye piece. The resolving power of telescope is thus limited by the size of objective lens and the minimum angle of resolution is given by 
.
Microscope In the case of microscope, we wish to measure the distance between object or see microstructure. However, unlike in the case of telescope, the objects are relatively at a short distance from objective lens. Let S1 and S2 are two objects (like light source, though these objects are not self luminous, light falling on them, after reflection reaches to the objective lens and the object behave like light source and I1and I2 are the images corresponding to them). The images will again be in the form of disk surrounded by dark and bright rings and these will be just resolved when Rayleigh criterion is satisfied i.e 
.
Or in other word when the first minima due to source S2 falls on the central maxima due to S1. i.e when the path difference between ray S2PI1 and S2QI1 is equal to 
(not 
as in the case of single slit but as for circular aperture). This path difference is equal to 
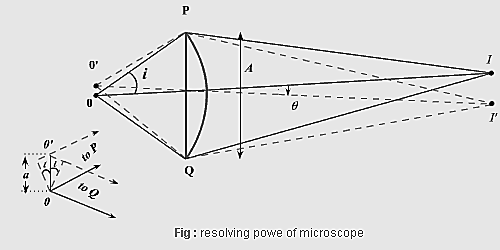(Fig.A.).
The image will be just resolved when
Where 
is the angle of the cone which source subtends on the objective lens. If the space between object and objective is filled with some liquid of refractive index n , the equation becomes
The term 
is known as numerical aperture as named by Abbe. Thus we see that the two closely spaced objects can be well resolved if either is small or n or is large.