Superposition Of Waves Of Slightly Different Wavelengths And Frequency: Interference
Superposition of waves of slightly different wavelengths and frequency: Let us now consider two light waves of frequency 
and wavelengths 
.The corresponding small wave vectors will be 
.
Again for the case of simplicity, let both the waves be propagating in same direction 
and let both have same state of polarization (i.e. their electric field vectors point along the 
axis) and amplitude 
.
The two waves can be written as
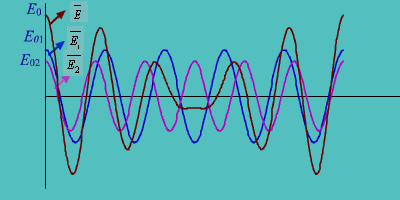
Fig.10.1.3:Resultant 
of two waves ( 
& 
) having different frequency (
) and wavelength.
The phase difference between these waves will vary in time as well as in space.
The resultant of two waves is given by
Using trigonometric relations
Thus we see that the resultant wave propagates with an average wave vector 
however the amplitude of such wave is modulated to form groups. The wave form of such individual waves and resultant wave is plotted in figure at t=0;
The individual waves, having the average of two k's correspond to the first cosine term in equation and their phase velocity(wave velocity) is given by
ie. the velocity is nearly the same as that of component waves. The envelope of modulation (wave packet) is given by the second cosine term. The wave vector for this is the difference of wave vector of two waves and is small, which corresponds to a larger wavelength. The velocity of the wave packet (group velocity) is given by
The wave velocity and group velocity are related as
where 
is the actual wavelength in the medium. For light waves traveling in vacuum there is no dispersion. (all waves move with same velocity), the wave and groups velocity is same.