Amperes Law

Amperes Law: Biot-Savart's law for magnetic field due to a current element is difficult to visualize physically as such elements cannot be isolated from the circuit which they are part of. Andre Ampere formulated a law based on Oersted's as well as his own experimental studies. Ampere's law states that `` the line integral of magnetic field around any closed path equals $\mu_0$ times the current which threads the surface bounded by such closed path. . Mathematically,

$\begin{displaymath}\oint\vec B\cdot\vec{dl} = \mu_0I_{enclosed}\eqno(1)\end{displaymath}$

In spite of its apparent simplicity, Ampere's law can be used to calculate magnetic field of a current distribution in cases where a lot of information exists on the behaviour of $\vec B$ . The field must have enough symmetry in space so as to enable us to express the left hand side of (1) in a functional form. The simplest application of Ampere' s law consists of applying the law to the case of an infinitely long straight and thin wire.

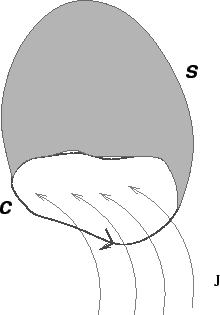
Ampere's Law in Differential Form: We may express Ampere's law in a differential form by use of Stoke's theorem, according to which the line integral of a vector field is equal to the surface integral of the curl of the field,

$\begin{displaymath}\oint \vec B\cdot\vec{dl} = \int_S{\rm curl}\; \vec B\cdot\vec{dS}\end{displaymath}$

The surface is any surface whose boundary is the closed path of integration of the line integral.

n terms of the current density $\vec J$ , we have, $\begin{displaymath}\int_S\vec J\cdot\vec{dS} = I_{encl}\end{displaymath}$

where $I_{encl}$ is the total current through the surface . Thus, Ampere's law $\oint\vec B\cdot\vec{dl} = I_{encl}$ is equivalent to

$\begin{displaymath}\int{\rm curl}\; \vec B\cdot\vec{dS} = \mu_0\int\vec J\cdot\vec{dS}\end{displaymath}$

which gives $\begin{displaymath}{\rm curl}\; \vec B = \mu_0\vec J\end{displaymath}$

You may recall that in the case of electric field, we had shown that the divergence of the field to be given by $\nabla\vec E = \rho/epsilon_0$ . In the case of magnetic field there are no free sources (monopoles). As a result the divergence of the magnetic field is zero $\begin{displaymath}\nabla\cdot\vec B =0\end{displaymath}$

The integral form of above is obtained by application of the divergence theorem

$\begin{displaymath}\int_S\vec B\cdot\vec{dS} = \int_V\nabla\cdot\vec B dV =0\end{displaymath}$

Thus the flux of the magnetic field through a closed surface is zero.