Biot- Savarts' Law

Biot- Savarts' Law: Biot-Savarts' law provides an expression for the magnetic field due to a current segment. The field $\vec{dB}$ at a position $\vec r$ due to a current segment $I\vec{dl}$ is experimentally found to be perpendicular to $\vec{dl}$ and $\vec r$ . The magnitude of the field is

proportional to the length $\mid dl\mid$ and to the current and to the sine of the angle between $\vec r$ and $\vec{dl}$ .
inversely proportional to the square of the distance of the point P from the current element.

$\begin{displaymath}\vec{dB} \propto I\frac{\vec{dl}\times\hat r}{r^2}\end{displaymath}$

In SI units the constant of proportionality is $\mu_0/4\pi$ , where $\mu_0$ is the permeability of the free space. The value of $\mu_0$ is

$\begin{displaymath}\mu_0 = 4\pi\times 10^{-7} \ \ {\rm N/amp}^2\end{displaymath}$

The expression for field at a point P having a position vector $\vec r$ with respect to the current element is

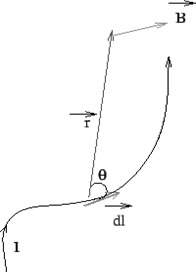
For a conducting wire of arbitrary shape, the field is obtained by vectorially adding the contributions due to such current elements as per superposition principle, $\begin{displaymath}\vec B(P) = \frac{\mu_0}{4\pi}I\int\frac{\vec{dl}\times\hat r}{r^2}\end{displaymath}$ where the integration is along the path of the current flow.