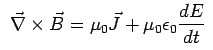←
Physics for Engineers - 2
Diamagnetism:displacement Current
Diamagnetism: Diamagnetism, being a consequence of Lenz's law is present in all substance though its effect may be masked because of other strong magnetic effects. However, certain substances like Bismuth are strongly diamagnetic. The effect arises because when an atom is placed in a magnetic field, the flux through the atomic orbit changes. This results in an induced current being generated which opposes the changing flux. The effect is equivalent to the atom developing an induced magnetic moment opposite to the direction of the applied field.
Displacement Current: We have seen that the magnetic field due to a current is given by Ampere's law
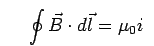
where the current passes through the surface of the boundary over which the above integral is taken. Maxwell pointed out that the equation is logically inconsistent.
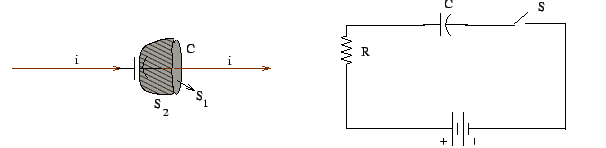
Consider a parallel plate capacitor being charged by a battery. During the process of charging a current passes through the terminals of the battery. The current produces a magnetic field around it. Consider an Amperian loop C located just outside one of the plates. Let the plane of the loop S1 be parallel to the plates. On applying Ampere's law to such a loop, we get the value of the above integral to be non-zero as there is a current passing through the wires. However, consider a second surface S1 which is located just inside the plates of the capacitor and does not intersect the wire at all. The flux of the current (the the surface integral of the current density) through this surface is zero. However, as both S1 and S2 are bounded by the same loop C, the flux through both must be the same. This is clearly inconsistent.
Consider a parallel plate capacitor being charged by a battery. During the process of charging a current passes through the terminals of the battery. The current produces a magnetic field around it. Consider an Amperian loop C located just outside one of the plates. Let the plane of the loop S1 be parallel to the plates. On applying Ampere's law to such a loop, we get the value of the above integral to be non-zero as there is a current passing through the wires. However, consider a second surface S1 which is located just inside the plates of the capacitor and does not intersect the wire at all. The flux of the current (the the surface integral of the current density) through this surface is zero. However, as both S1 and S2 are bounded by the same loop C, the flux through both must be the same. This is clearly inconsistent.
To remove the apparent inconsistency, we need to revise our notion of what constitutes a current. We generally believe that current being a flow of charge must be the same at all cross sections of a series circuit. This is obviously not true for circuits containing capacitors. Consider an RC circuit. When the switch S is closed, the capacitor charges and the current is given by
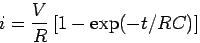
This does not hold inside the capacitor as the dielectric between the plates is a dielectric (could be air) and does not conduct electricity. In order to preserve the continuity of current inside the dielectric, we need to reconcile the apparent inconsistency. Since the current through the wire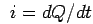 
is the rate of flow of charge through the wires, we may express it in terms of the electric field inside the capacitor plates. Since the electric field inside the capacitor is given by 
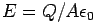, an equivalent expression for current is
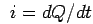is the rate of flow of charge through the wires, we may express it in terms of the electric field inside the capacitor plates. Since the electric field inside the capacitor is given by 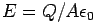, an equivalent expression for current is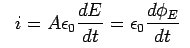
where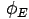 
is the electric flx through the capacitor.
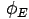is the electric flx through the capacitor.
Maxwell suggested that a term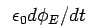 
should be considered as current through the dielectric. He termed this current as displacement current. The Ampere's law is modified to read
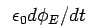should be considered as current through the dielectric. He termed this current as displacement current. The Ampere's law is modified to read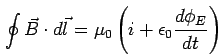
Equation above is now logically consistent because inside the dielectric 
and the value of the integral is given by the second term. The current exists whenever the electric field, and hence the electric flux, is changing with time. Using Stoke's theorem, we may convert the above to a differential form
and the value of the integral is given by the second term. The current exists whenever the electric field, and hence the electric flux, is changing with time. Using Stoke's theorem, we may convert the above to a differential form