Dielectric Constant And Polarizability

Dielectric constant and polarizability: The dielectric constant e of an isotropic or cubic medium relative to vacuum is defined in terms of
the macroscopic field E:

Since the polarization of the medium is produced by the field it is convenient to define the polarizability a of an atom in terms of the local electric field at the atom:

where p is the dipole moment. For a non-spherical atom α will be a tensor. The polarization of a crystal may be expressed approximately as the product of the polarizabilities of the atoms times the local electric field:

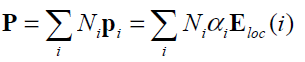......................1

where N_i is the concentration and α_i the polarizability of atoms i, and E_loc(i) is the local field at atom sites i.

We want to relate the dielectric constant to the polarizabilities; the result will depend on the relation that holds between the macroscopic electric field and the local electric field. If the local field is given by the Lorentz relation, then

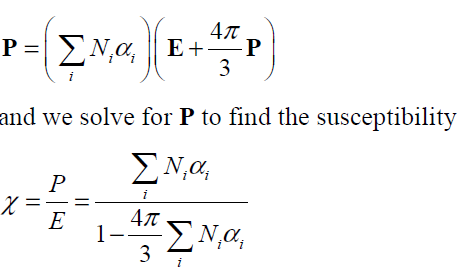............................2& 3

Using Eq.(1) we can then write the expression in terms of the dielectric constant:

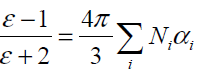
This is the Clausius-Mossotti relation. This relates the dielectric constant to the electronic polarizability, but only for crystal structures for which the Lorentz local field holds.