Force On A Current Carrying Conductor

Force on a Current Carrying Conductor: A conductor has free electrons which can move in the presence of a field. Since a magnetic field exerts a force $q\vec v\times\vec B$ on a charge moving with a velocity $\vec v$ , it also exerts a force on a conductor carrying a current.

Consider a conducting wire carrying a current . The current density at any point in the wire is given by'

$\begin{displaymath}\vec J = ne\vec v\end{displaymath}$

where

is the number density of electrons having a charge

each and $\vec v$ is the average drift velocity at that point.

Consider a section of length

of the wire. If

is the cross sectional area of the section oriented perpendicular to the direction of $\vec J$ , the force on the electrons in this section is
$\begin{displaymath}d\vec F = dq\vec v\times\vec B\end{displaymath}$

where

is the amount of charge in the section

$\begin{displaymath}dq = neAdl\end{displaymath}$

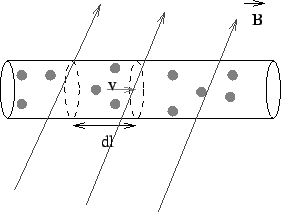
Thus the force on the conductor in this section is $\begin{displaymath}d\vec F = neA dl \vec v\times\vec B\end{displaymath}$

If $\vec{dl}$ represents a vector whose magnitude is the length of the segment and whose direction is along the direction of $\vec v$ , we may rewrite the above as

$\begin{eqnarray*} d\vec F &=& neAv\vec{dl}\times\vec B\\ &=& JA \vec{dl}\times\vec B\\ &=& I \vec{dl}\times\vec B \end{eqnarray*}$

The net force on the conductor is given by summing over all the length elements. If $\hat u_l$ denotes a unit vector in the direction of the current, then $\begin{displaymath}\vec F = I \int \hat u_l\times\vec B dl\end{displaymath}$