Piezoelectricity
Piezoelectricity: The term piezoelectricity refers to the fact that, when a crystal is strained, an electric field is produced within the substance. As a result of this field, a potential difference develops across the sample, and by measuring this potential one may determine the field. The inverse effect - that an
applied field produces strain - has also been observed.
The piezoelectric effect is very small. A field of 103 V/cm in quartz (SiO2) produces a strain of only 10-7. That is, a rod 1 cm long changes its length by 10Å. Conversely, even small strains can produce enormous electric fields.
The piezoelectric effect is often used to convert electrical energy into mechanical energy, and vice versa; i.e., the substance is used as a transducer. For instance, an electric signal applied to the end of a quartz rod generates a mechanical strain, which consequently leads to the propagation of a mechanical wave - a sound wave - down the rod. Quartz is the most familiar piezoelectric substance, and the one most frequently used in transducers.
The microscopic origin of piezoelectricity lies in the displacement of ionic charges within the crystal. In the absence of strain, the distribution of the charges at their lattice sites is symmetric, so the internal electric field is zero. But when the crystal is strained, the charges are displaced. If the charge distribution is no longer symmetric, then a net polarization, and a concomitant electric field, develops. It is this field which operates in the piezoelectric effect.
 \
\
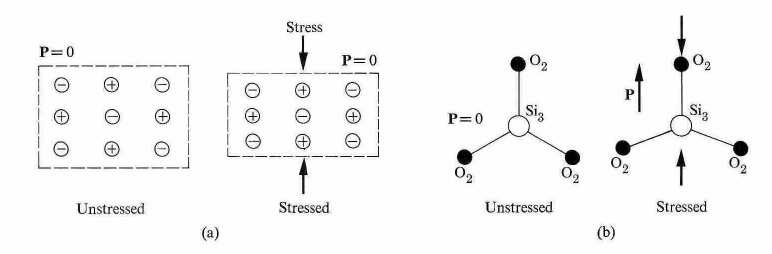
Fig. 1Crystal with center of inversion exhibits no piezoelectric effect, (b) Origin of piezoelectric effect in quartz: crystal lacks a center of inversion.
It follows that a substance can be piezoelectric only if the unit cell lacks a center of inversion. Figure 1 (a) shows this, and demonstrates that if a center of inversion is present, it persists even after distortion, and consequently the polarization remains zero. However, when there is no center of inversion, as in Fig. 1 (b), distortion produces a polarization. We see, therefore, that no regular cubic lattice can exhibit piezoelectricity.
The lack of inversion center, however, is not sufficient to guarantee piezoelectricity, and only relatively few substances, exhibit this phenomenon.