Potential Energy Of A Magnetic Dipole

Potential Energy of a Magnetic Dipole: A current loop does not experience a net force in a magnetic field. It however, experiences a torque. This is very similar to the behaviour of an electric dipole in an electric field. A current loop, therefore, behaves like a magnetic dipole.
We define the magnetic dipole moment 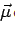of a current loop to be a vector of magnitude

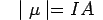
and direction perpendicular to the plane of the loop (as determined by right hand rule). If the loop has 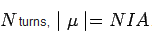. In a magnetic field, the dipole experiences a torque

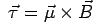
The form of torque suggests that in a magnetic field the dipole tends to align parallel to the field. If the orientation of the dipole is at some angle θ to the field, there must be some potential energy stored in the dipole. This is because, if we wish to bring the dipole from θ  = 0 to some arbitrary angle θ , we have to oppose the torque due to the field and do work in the process.

The work done is given by

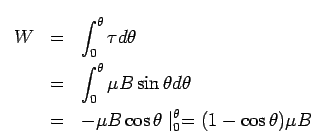
This amount of work is stored as the additional potential energy of the dipole. In analogy with the case of electric dipole in an electric field, the potential energy of the magnetic dipole in a magnetic field is given by

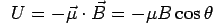
The energy is lowest when 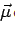and 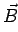are along the same direction and is maximum when they are anti-parallel.