←
Physics for Engineers - 2
Self Inductance
Self Inductance: Even when there is a single circuit carrying a current, the magnetic field of the circuit links with the circuit itself. If the current happens to be time varying, an emf will be generated in the circuit to oppose the change in the flux linked with the circuit. The opposing voltage acts like a second voltage source connected to the circuit. This implies that the primary source in the circuit has to do additional work to overcome this back emf to establish the same current. The induced current has a direction determined by Lenz's law.
If no ferromagnetic materials are present, the flux is proportional to the current. If the circuit contains N turns, Faraday's law gives
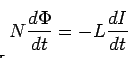
where L is known as Self Inductance of the circuit. By definition, L is a positive quantity. From the above it follows, on integrating,
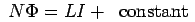
Since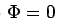 
when 
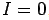, the constant is zero and we get
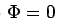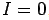when , the constant is zero and we get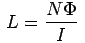
The self inductance can, therefore, interpreted as the amount of flux linked with the circuit for unit current. The emf is given by
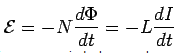
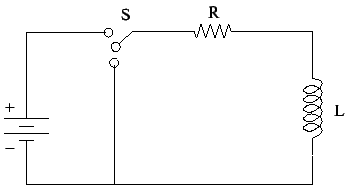
Energy Stored in Magnetic Fiel: Just as capacitor stores electric energy, an inductor can store magnetic energy. To see this consider an L-R circuit in which a current I0 is established. If the switch is thrown to the position such that the battery gets disconnected from the circuit at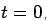 
, the current in the circuit would decay. As the inductor provides back emf, the circuit is described by
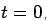, the current in the circuit would decay. As the inductor provides back emf, the circuit is described by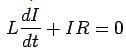
With the initial condition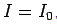 
, the solution of the above is
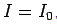, the solution of the above is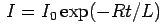
As the energy dissipated in the circuit in time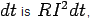
the total energy dissipated from the time the battery is disconnected is
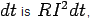the total energy dissipated from the time the battery is disconnected is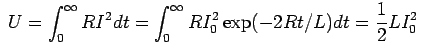
Thus the energy initially stored must have been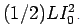 
. If an inductor carries a current L , it stores an energy 
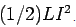. Thus the toroidal inductor discussed earlier stores an energy
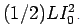. If an inductor carries a current L , it stores an energy 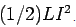. Thus the toroidal inductor discussed earlier stores an energy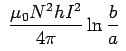
when it carries a current I. We eill now show that this is also equal to the volume integral of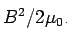 
.
.
Consider the magnetic field in the toroid at a distance 
from the axis. We have seen that the magnetic field B is given by 
. Thus the value of 
at this distance is 
. Considering the toroid to consist of shells of surface area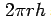 
and thickness 
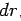the volume of the shell is 
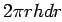. The volume integral of 
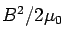is therefore,
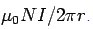from the axis. We have seen that the magnetic field B is given by . Thus the value of 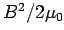at this distance is 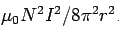. Considering the toroid to consist of shells of surface area 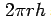and thickness 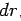the volume of the shell is 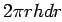. The volume integral of 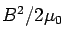is therefore,
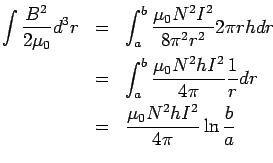which is exactly the expression for the stored energy derived earlier.