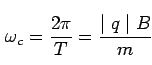The Lorentz Force

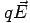The Lorentz Force: We know that an electric field exerts a force on a charge 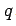. In the presence of a magnetic field 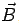, a charge q experiences an additional force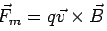

where 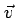is the velocity of the charge. Note that

• There is no force on a charge at rest.
• A force is exerted on the charge only if there is a component of the magnetic field perpendicular to the direction of the velocity, i.e. the component of the magnetic field parallel to 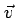does not contribute to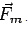

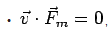•  , which shows that the magnetic force does not do any work. In the case where both 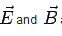are present, the force on the charge q is given by

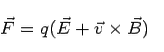
This is called Lorentz force after H.E. Lorentz who postulated the relationship. It may be noted that the force expression is valid even when 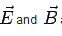are time dependent

Unit of Magnetic Field: From the Lorentz equation, it may be seen that the unit of magnetic field is Newton-second/coulomb-meter, which is known as a Tesla (T). (The unit is occasionally written as Weber/m as the unit of magnetic flux is known as Weber). However, Tesla is a very large unit and it is common to measure 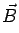in terms of a smaller unit called Gauss,

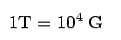
It may be noted that 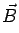is also referred to as magnetic field of induction or simply as the induction field. However, we will use the term ``magnetic field".

Motion of a Charged Particle in a Uniform Magnetic Field: Let the direction of the magnetic field be taken to be z- direction,

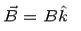
we can write the force on the particle to be

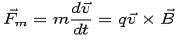
The problem can be looked at qualitatively as follows. We can resolve the motion of the charged particle into two components, one parallel to the magnetic field and the other perpendicular to it. Since the motion parallel to the magnetic field is not affected, the velocity component in the z-direction remains constant.

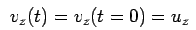
where U is the initial velocity of the particle. Let us denote the velocity component perpendicular to the direction of the magnetic field by 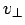. Since the force(and hence the acceleration) is perpendicular to the direction of velocity, the motion in a plane perpendicular to 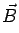is a circle. The centripetal force necessary to sustain the circular motion is provided by the Lorentz force

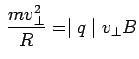
where the radius of the circle R is called the Larmor radius, and is given by

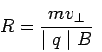
The time taken by the particle to complete one revolution is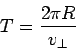

The cyclotron frequency 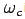is given by