Constant Utilization Server Algorithm
Constant Utilization Server Algorithm
We now return our attention to the problem of scheduling aperiodic jobs amid periodic tasks in a deadline-driven system. For the purpose of executing aperiodic jobs, there is a basic constant utilization server. The server is defined by its size, which is its instantaneous utilization ˜ us ; this fraction of processor time is reserved for the execution of aperiodic jobs. As with deferrable servers, the deadline d of a constant utilization server is always defined. It also has an execution budget which is replenished according to the replenishment rules described below. The server is eligible and ready for execution only when its budget is nonzero. When the server is ready, it is scheduled with the periodic tasks on the EDF basis. While a sporadic server emulates a periodic task, a constant utilization server emulates a sporadic task with a constant instantaneous utilization, and hence its name.
Consumption and Replenishment Rules. The consumption rule of a constant utilization server, as well as that of a total bandwidth or weighted fair-queueing server, is quite simple. A server consumes its budget only when it executes. You will see shortly that such a server never has any budget when there is no aperiodic job ready for execution. Hence the problem of dealing with chunks of budget never arises.
The budget of a basic constant utilization server is replenished and its deadline set according to the following rules. In the description of the rules, ˜ us is the size of the server, es is its budget, and d is its deadline. t denotes the current time, and e denotes the execution time of the job at the head the aperiodic job queue. The job at the head of the queue is removed when it completes. The rules assume that the execution time e of each aperiodic job becomes known when the job arrives. We will return later to discuss how to remove this restriction. Replenishment Rules of a Constant Utilization Server of Size ˜ us
R1 Initially, es = 0, and d = 0.
R2 When an aperiodic job with execution time e arrives at time t to an empty aperiodic job queue,
(a) if t < d, do nothing;
(b) if t ≥ d, d = t e/ ˜ us, and es = e.
R3 At the deadline d of the server,
(a) if the server is backlogged, set the server deadline to d e/ ˜ us and es = e;
(b) if the server is idle, do nothing.
In short, a constant utilization server is always given enough budget to complete the job at the head of its queue each time its budget is replenished. Its deadline is set so that its instantaneous utilization is equal to ˜ us .
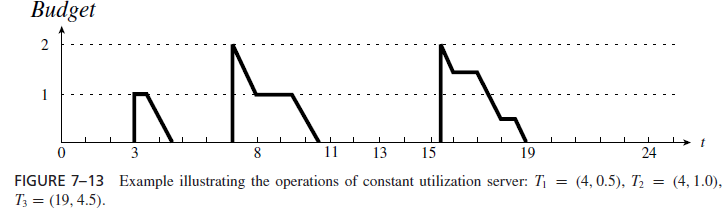
Figure 7–13 illustrates how a constant utilization server works. This system of periodic tasks and aperiodic jobs is essentially the same as the system in Figure 7–8. (For this system, the simple fixed-priority and deadline-driven sporadic servers happen to behave the same.) The only difference between them is that in Figure 7–13, aperiodic job A2 arrives at time 6.9 instead of 7.0. The size of the constant utilization server is 0.25, slightly smaller than the size of the sporadic server in Figure 7–8.
1. Before time 3.0, the budget of the server is 0. Its deadline is 0. The server does not affect other tasks because it is suspended.
2. At time 3, A1 arrives. The budget of the server is set to 1.0, the execution time of A1, and its deadline is 3 1.0/0.25 = 7 according to R2b. The server is ready for execution. It completes A1 at time 4.5.
3. When A2 arrives at time 6.9, the deadline of the server is later than the current time. According to R2a, nothing is done except putting A2 in the aperiodic job queue.
4. At the next deadline of the server at 7, the aperiodic job queue is checked and A2 is found waiting. The budget of the server is replenished to 2.0, the execution time of A2, and its deadline is 7 2.0/0.25 = 15. The server is scheduled and executes at time 7, is preempted by T2 at time 8, resumes execution at 9.5 and completes A2 at time 10.5.
5. At time 15, the aperiodic job queue is found empty. Nothing is done.
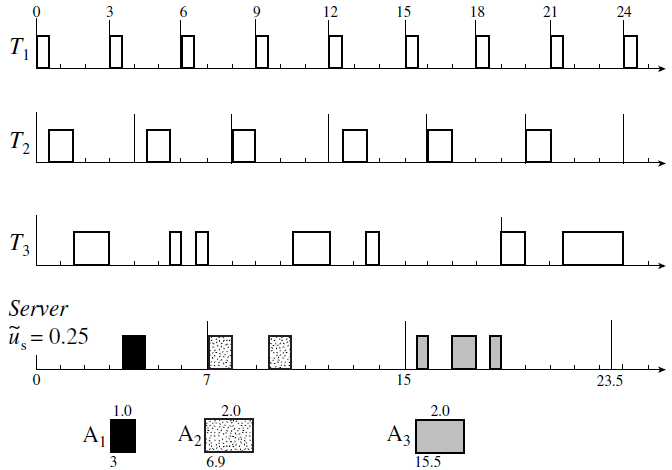
6. At time 15.5, A3 arrives. At the time, the deadline of the server is 15. Hence according
to rule R2b, its deadline is set at 23.5, and the server budget is set to 2.0. This allows
the server to execute A3 to completion at time 19.
We see that the constant utilization server completes each of the aperiodic jobs earlier than a simple sporadic server.
Scheduling Aperiodic Jobs with Unknown Execution Times. In the description of
the constant utilization server algorithm, we assume that the execution times of aperiodic jobs become known upon their arrival. This restrictive assumption can be removed by modifying the replenishment rules of constant utilization (or total bandwidth) servers. One way is to give the server a fixed size budget es and fixed period es/ ˜ us just like sporadic and deferrable servers. Since the execution time of each aperiodic job can be determined after it is completed with little overhead, we can adjust the server deadline based on this knowledge upon the completion of the job. Specifically, when an aperiodic job with execution time e shorter than es completes, we reduce the current deadline of the server by (es − e)/ ˜ us units before replenishing the next es units of budget and setting the deadline accordingly. This action clearly can improve the performance of the server and does not make the instantaneous utilization of the server larger than ˜ us .
An aperiodic job with execution time larger than es is executed in more than one server period.We can treat the last chunk of such a job in the manner described above if the execution time of this chunk is less than es