Effective Release Times And Deadlines

EFFECTIVE RELEASE TIMES AND DEADLINES
The given release times and deadlines of jobs are sometimes inconsistent with the precedence constraints of the jobs. By this, we mean that the release time of a job may be later than that of its successors, and its deadline may be earlier than that of its predecessors. Therefore, rather than working with the given release times and deadlines, we first derive a set of effective release times and deadlines from these timing constraints, together with the given precedence constraints. The derived timing constraints are consistent with the precedence constraints. When there is only one processor, we can compute the derived constraints according to the following rules:

Effective Release Time: The effective release time of a job without predecessors is equal to its given release time. The effective release time of a job with predecessors is equal to the maximum value among its given release time and the effective release times of all of its predecessors.

Effective Deadline: The effective deadline of a job without a successor is equal to its given deadline. The effective deadline of a job with successors is equal to the minimum value among its given deadline and the effective deadlines of all of its successors. The effective release times of all the jobs can be computed in one pass through the precedence graph in O(n2) time where n is the number of jobs. Similarly, the effective deadlines can be computed in O(n2) time.

As an example, we look at the set of jobs in Figure 4–3. The numbers in the parentheses next to the name of each job are its given release times and deadlines. Because J1 and J2 have no predecessors, their effective release times are the given release times, that is, 2 and 0, respectively. The given release time of J3 is 1, but the latest effective release time of its predecessors is 2, that of J1. Hence, the effective release time of J3 is 2. You can repeat this procedure and find that the effective release times of the rest of the jobs are 4, 2, 4, and 6, respectively. Similarly, J6 and J7 have no successors, and their effective deadlines are equal to their given deadlines, 20 and 21, respectively. Since the effective deadlines of the successors of J4 and J5 are larger than the given deadlines of J4 and J5, the effective deadlines of J4 and J5 are equal to their given deadlines. On the other hand, the given deadline of J3 is equal to 12, which is larger than the minimum value of 8 among the effective deadlines of its successors. Hence, the effective deadline of J3 is 8. In a similar way, we find that the effective deadlines of J1 and J2 are 8 and 7, respectively.

You may have noticed that the calculation of effective release times and deadlines does not take into account the execution times of jobs. More accurately, the effective deadline of a job should be as early as the deadline of each of its successors minus the execution time of the successor. The effective release time of a job is that of its predecessor plus the execution time of the predecessor. The more accurate calculation is unnecessary, however, when there is only one processor. Gary and Johnson [GaJo77] have shown that it is feasible to schedule any

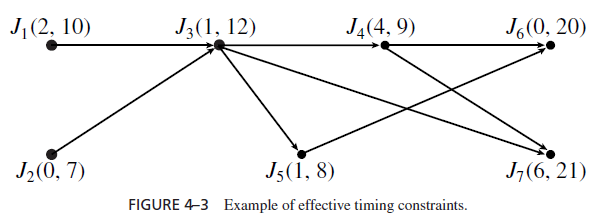
set of jobs on a processor according to their given release times and deadlines if and only if it is feasible to schedule the set according to their effective release times and deadlines defined above.When there is only one processor and jobs are preemptable, working with the effective release times and deadlines allows us to temporarily ignore the precedence constraints and treat all the jobs as if they are independent. Of course, by doing so, it is possible for an algorithm to produce an invalid schedule that does not meet some precedence constraint. For example, J1 and J3 in Figure 4–3 have the same effective release time and deadline. An algorithm which ignores the precedence constraint between them may schedule J3 in an earlier interval and J1 in a later interval. If this happens, we can always add a step to swap the two jobs, that is, move J1 to where J3 is scheduled and vice versa. This swapping is always possible, and it transforms an invalid schedule into a valid one.

Hereafter, by release times and deadlines, we will always mean effective release times and deadlines. When there is only one processor and jobs are preemptable, we will ignore the precedence constraints.