Fairness And Starvation

Fairness and Starvation:By a scheduling algorithm being fair within a time interval, we mean that the fraction time of processor time in the interval attained by each server that is backlogged throughout the interval is proportional to the server size. For many applications (e.g., data transmission in switched networks), fairness is important.

It is well known in communication literature that the virtual clock algorithm (i.e., nonpreemptive total bandwidth server algorithm) is unfair. To illustrate that this is also true for the total bandwidth server algorithm, let us consider a system consisting solely of two total bandwidth servers, TB1 and TB2, each of size 0.5. Each server executes an aperiodic task; jobs in the task are queued in the server’s own queue. It is easy to see that if both servers are never idle, during any time interval of length large compared to the execution times of their jobs, the total amount of time each server executes is approximately equal to half the length of the interval. In other words, each server executes for its allocated fraction of time approximately.

Now suppose that in the interval (0, t), for some t > 0, server TB1 remains backlogged, but server TB2 remains idle. By time t , TB1 have executed for t units of time and its deadline is at least equal to 2t . If at time t , a stream of jobs, each with execution time small compared with t , arrives and keeps TB2 backlogged after t . In the interval (t, 2t), the deadline of TB2 is earlier than the deadline of TB1. Hence, TB2 continues to execute, and TB1 is starved during this interval. While processor time is allocated fairly during (0, 2t), the allocation is unfair during (t, 2t). Since t is arbitrary, the duration of unfairness is arbitrary. As a consequence, the response time of jobs executed by TB1 can arbitrarily be large after t . This is not acceptable for many applications. (An example is an aperiodic task that is executed in response to keyboard entries of a video game. The player will not happy if the system becomes sluggish for a considerable length of time, no matter how responsive it was in the past.)

In the remainder of this section, we first formally define fairness and then present two solutions. We will discuss this issue further in Chapter 11 which is on real-time communication.

Definition of Fairness. Since fairness is not an important issue for periodic tasks, we confine our attention here to systems containing only aperiodic and sporadic jobs. Specifically, we consider a system consisting solely of n (> 1) servers. Each server executes an aperiodic
or sporadic task. For i = 1, 2, . . . , n, the size of the ith server is ˜ ui .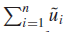 is no greater than 1, and hence every server is schedulable. ˜wi (t1, t2), for 0 < t1 < t2, denotes the total attained processor time of the ith server in the time interval (t1, t2), that is, the server executes for ˜wi (t1, t2) units of time during this interval. The ratio ˜wi (t1, t2)/ ˜ ui is called the normalized service attained by the ith server. A scheduler (or the scheduling algorithm used by the scheduler) is fair in the interval (t1, t2) if the normalized services attained by all servers that are backlogged during the interval differ by no more than the fairness threshold FR ≥ 0. In the ideal case, FR is equal to zero, and

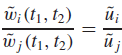
for any t2 > t1 and ith and j th servers that are backlogged throughout the time interval (t1, t2). Equivalently,

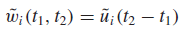
It should not be a surprise that only an algorithm that infinitesmally fine-grain time slices among ready servers can achieve ideal fairness. Hence, ideal fairness is not realizable in practice. For a given scheduling algorithm, the difference in the values of the two sides of the above expression depends on the length t2 − t2 of the time interval over which fairness is measured. In general, FR is a design parameter. By allowing processor time allocation to be somewhat unfair (i.e., for some acceptable FR > 0) over some time interval length, we admit simple and practical schemes to keep scheduling fair.

Elimination of Starvation. Let us examine again the previous example of two total bandwidth servers. The starvation problem is due to the way in which the total bandwidth server algorithm makes background time available to TB1; in general, the deadline of a backlogged total bandwidth server is allowed to be arbitrarily far in the future when there is spare processor time. The simple scheme presented below, as well as the weighted fair-queueing algorithm presented in the next subsection, eliminates starvation and improve fairness by keeping the deadlines of backlogged servers sufficiently close to the current time.

A simple solution is to use only constant utilization servers. Since the budget of such a server is never replenished before the current server deadline, the current deadline of a backlogged constant utilization server CUi of size ˜ ui is never more than ei,max/ ˜ ui units of time from the current time. (ei,max is the maximum execution time of all the jobs executed by the server.) Hence the length of starvation suffered by any server is bounded by maxi (ei,max/ ˜ ui ).To allow these servers to use background time.

Replenishment Rules of a Starvation-Free Constant Utilization/Background Server:

R1 –R3 Within any busy interval of the system, replenish the budget of each backlogged server following rules of a constant utilization server.
R4 Whenever a busy interval of the system ends, replenish the budgets of all backlogged servers.

To illustrate, we look at the example in Figure 7–14. The system contains four aperiodic tasks A1, A2, A3, and A4, each a stream of jobs with identical execution times. Specifically,