Introduction To Real Time Systems

Introduction: The correctness of many systems and devices in our modern society depends not only on the effects or results they produce but also on the time at which these results are produced. These real-time systems range from the anti-lock braking controller in automobiles to the vital-sign monitor in hospital intensive-care units. For example, when the driver of a car applies the brake, the anti-lock braking controller analyzes the environment in which the controller is embedded (car speed, road surface, direction of travel) and activates the brake with the appropriate frequency within fractions of a second. Both the result (brake activation) and the time at which the result is produced are important in ensuring the safety of the car, its driver, and passengers.

Recently, computer hardware and software are increasingly embedded in a majority of these real-time systems to monitor and control their operations. These computer systems are called embedded systems, real-time computer systems, or simply real-time systems. Unlike conventional, non-real-time computer systems, real-time computer systems are closely coupled with the environment being monitored and controlled. Examples of real-time systems include computerized versions of the braking controller and the vital-sign monitor, the new generation of airplane and spacecraft avionics, the planned Space Station control software, highperformance network and telephone switching systems, multimedia tools, virtual reality systems, robotic controllers, battery-powered instruments, wireless communication devices (such as cellular phones and PDAs), astronomical telescopes with adaptive-optics systems, and many safety-critical industrial applications. These embedded systems must satisfy stringent timing and reliability constraints in addition to functional correctness requirements.

Figure 1.1 shows a model of a real-time system. A real-time system has a decision component that interacts with the external environment (in which the decision

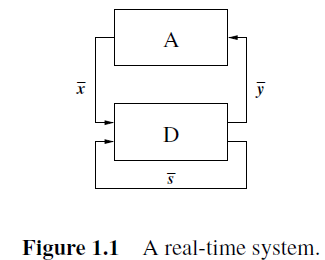
component is embedded) by taking sensor readings and computing control decisions based on sensor readings and stored state information.We can characterize this realtime system model with seven components:
1. A sensor vector ¯ x ∈ X,
2. A decision vector ¯y ∈ Y ,
3. A system state vector ¯s ∈ S,
4. A set of environmental constraints A,
5. A decision map D, D : S × X → S × Y ,
6. A set of timing constraints T , and
7. A set of integrity constraints I .

In this model, X is the space of sensor input values, Y is the space of decision values, and S is the space of system state values. Let ¯ x(t) denote the value of the
sensor input ¯ x at time t , and so on.

The environmental constraints A are relations over X, Y , S and are assertions about the effect of a control decision on the external world which in turn affect future sensor input values. Environmental constraints are usually imposed by the physical environment in which the real-time decision system functions. The decision map D relates ¯y(t 1), ¯s(t 1) to ¯ x(t ), ¯s(t), that is, given the current system state and sensor input, D determines the next decisions and system state
values. Decision maps can be implemented by computer hardware and software components. A decision system need not be centralized, and may consist of a network of coordinating, distributed monitoring/decision-making components.

The decisions specified by D must conform to a set of integrity (safety) constraints I . Integrity constraints are relations over X, S, Y and are assertions that the decision map D must satisfy to ensure safe operation of the physical system under control. The implementation of the decision map D is subject to a set of timing constraints T , which are assertions about how fast the map D has to be performed. In addition, timing constraints exist on the environment (external to the decision system) that must be satisfied for the correct functioning of this environment.

There are two ways to ensure system safety and reliability. One way is to employ engineering (both software and hardware) techniques, such as structured programming principles, to minimize implementation errors and then utilize testing techniques to uncover errors in the implementation. The other way is to use formal analysis and verification techniques to ensure that the implemented system satisfy the required safety constraints under all conditions given a set of assumptions. In a realtime system, we need to not only satisfy stringent timing requirements but also guard against an imperfect execution environment, which may violate pre-runtime design assumptions. The first approach can only increase the confidence level we have on the correctness of the system because testing cannot guarantee that the system is error-free [Dahl, Dijkstra, and Hoare, 1972]. The second approach can guarantee that a verified system always satisfies the checked safety properties, and is the focus of this text.

However, state-of-the-art techniques, which have been demonstrated in pedagogic systems, are often difficult to understand and to apply to realistic systems. Furthermore, it is often difficult to determine how practical a proposed technique is from the large number of mathematical notations used. The objective of this book is to provide a more readable introduction to formal techniques that are practical for actual use. These theoretical foundations are followed by practical exercises in employing these advanced techniques to build, analyze, and verify different modules of real-time systems. Available specification analysis and verification tools are also described to help design and analyze real-time systems.