Nonpreemptive Critical Sections

NONPREEMPTIVE CRITICAL SECTIONS: The simplest way to control access of resources is to schedule all critical sections on the processor nonpreemptively [Mok]. (In other words, when a job requests a resource, it is always allocated the resource. When a job holds any resource, it executes at a priority higher than the priorities of all jobs.) This protocol is called the Nonpreemptive Critical Section (NPCS) protocol. Because no job is ever preempted when it holds any resource, deadlock can never occur.

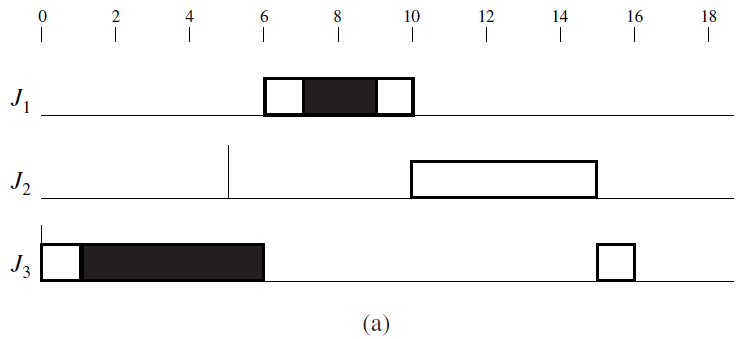
Take the jobs in Figure 8–4 for example. Figure 8–7(a) shows the schedule of these jobs when their critical sections are scheduled nonpreemptively on the processor. According to this schedule, J1 is forced to wait for J3 when J3 holds the resource. However, as soon as J3 releases the resource, J1 becomes unblocked and executes to completion. Because J1 is not delayed by J2, it completes at time 10, rather than 15 according to the schedule in Figure 8–4.

In general, uncontrolled priority inversion illustrated by Figure 8–4 can never occur. The reason is that a job Jh can be blocked only if it is released when some lower-priority job is in a critical section. If it is blocked, once the blocking critical section completes, all resources are free. No lower-priority job can get the processor and acquire any resource until Jh completes. Hence, Jh can be blocked only once, and its blocking time due to resource conflict is at most equal to the maximum execution time of the critical sections of all lower-priority jobs.

Specifically, the blocking time bi (rc) due to resource conflict of a periodic task Ti in a fixed-priority system of n periodic tasks is equal to

when the tasks are indexed in order of nonincreasing priority. In a system where periodic tasks are scheduled on the EDF basis, a job in task Ti with relative deadline Di can be blocked only by jobs in tasks with relative deadlines longer than Di . This was stated in Theorem 6.18. Therefore, the blocking time bi (rc) of Ti is again given by Eq. (8.1) if we index the periodic tasks according to their relative deadlines so that i < j if Di < Dj .

As an example, suppose that the tasks in the system in Figure 8–6(b) are scheduled on a fixed-priority basis. The blocking time b1(rc) of the highest priority task T1 is 8, the execution time of the (outermost) critical section of T3. Similarly, b2(rc) is 8, while b3(rc) is 2, the execution time of the critical section of T4. No task blocks T4 since it has the lowest

priority. Suppose that the relative deadlines of the tasks are D1 < D2 < D3 < D4 and the tasks are scheduled on an EDF basis. Then the blocking times bi (rc) for i = 1, 2, 3, and 4 are also 8, 8, 2, and 0, respectively.

The most important advantage of the NPCS protocol is its simplicity, especially when the numbers of resource units are arbitrary. The protocol does not need any prior knowledge about resource requirements of jobs. It is simple to implement and can be used in both fixed-priority and dynamic-priority systems. It is clearly a good protocol when all the critical sections are short and when most of the jobs conflict with each other.

An obvious shortcoming of this protocol is that every job can be blocked by every lower-priority job that requires some resource even when there is no resource conflict between them. When the resource requirements of all jobs are known, an improvement is to let a job holding any resource execute at the highest priority of all jobs requiring the resource. This is indeed how the ceiling-priority protocol supported by the Real-Time Systems Annex of Ada95 [Cohe96] works. We will discuss the ceiling-priority protocol and its worst-case performance in detail in Section 8.6, after examining two other well-known protocols that aim at improving upon the NPCS protocol.