Precedence Constraints And Data Dependency
PRECEDENCE CONSTRAINTS AND DATA DEPENDENCY: Data and control dependencies among jobs may constrain the order in which they can execute. In classical scheduling theory, the jobs are said to have precedence constraints if they are constrained to execute in some order. Otherwise, if the jobs can execute in any order, they are said to be independent.
For example, in a radar surveillance system, the signal-processing task is the producer of track records, while the tracker task is the consumer. In particular, each tracker job processes the track records generated by a signal-processing job. The designer may choose to synchronize the tasks so that the execution of the kth tracker job does not begin until the kth signal-processing job completes. The tracker job is precedence constrained. In general, a consumer job has this constraint whenever it must synchronize with the corresponding producer job(s) and wait until the latter completes in order to execute.
As another example, we consider queries to an information server. Suppose that before each query is processed and the requested information retrieved, its authorization to access the requested information is first checked. The retrieval job cannot begin execution until the authentication job completes. The communication job that forwards the information to the requester cannot begin until the retrieval job completes. Similarly, in a communication system, the jobs that generate an acknowledgement of a message and transmit the acknowledgement message cannot begin until the job that receives and processes the message completes.
Precedence Graph and Task Graph
We use a partial-order relation <, called a precedence relation, over the set of jobs to specify the precedence constraints among jobs. A job Ji is a predecessor of another job Jk (and Jk a successor of Ji) if Jk cannot begin execution until the execution of Ji completes. A shorthand notation to state this fact is Ji < Jk . Ji is an immediate predecessor of Jk (and Jk is an immediate successor of Ji) if Ji < Jk and there is no other job Jj such that Ji < Jj < Jk. Two jobs Ji and Jk are independent when neither Ji < Jk nor Jk < Ji . A job with predecessors is ready for execution when the time is at or after its release time and all of its predecessors are completed.
A classical way to represent the precedence constraints among jobs in a set J is by a directed graph G = (J,<). Each vertex in this graph represents a job in J. We will call each vertex by the name of the job represented by it. There is a directed edge from the vertex Ji to the vertex Jk when the job Ji is an immediate predecessor of the job Jk . This graph is called a precedence graph.
A task graph, which gives us a general way to describe the application system, is an extended precedence graph. Figure 3–1 shows a task graph. As in a precedence graph, the vertices in a task graph represent jobs. They are shown as circles and squares in this figure. (Here, we ignore the difference between the types of jobs represented by them. The need
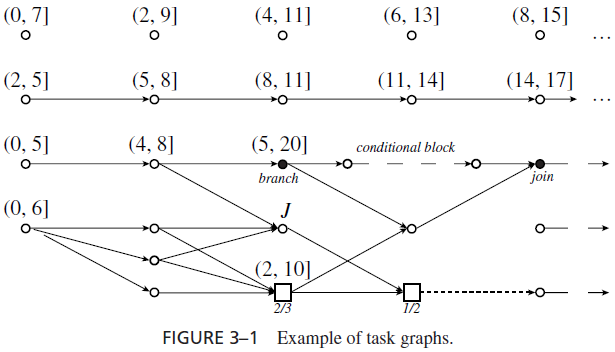
to differentiate them arises only in the next section.) For simplicity, we show only the job attributes that are of interest to us. The numbers in the bracket above each job give its feasible interval. The edges in the graph represent dependencies among jobs. If all the edges are precedence edges, representing precedence constraints, then the graph is a precedence graph.
Specifically, the system described by the graph in Figure 3–1 includes two periodic tasks. The task whose jobs are represented by the vertices in the top row has phase 0, period 2, and relative deadline 7. The jobs in it are independent; there are no edges to or from these jobs. In other words, the jobs released in later periods are ready for execution as soon as they are released even though some job released earlier is not yet complete. This is the usual assumption about periodic tasks. The vertices in the second row of Figure 3–1 represent jobs in a periodic task with phase 2, period 3, and relative deadline 3. The jobs in it are dependent; the first job is the immediate predecessor of the second job, the second job is the immediate predecessor of the third job, and so on. The precedence graph of (the jobs in) this task is a chain as shown here. A subgraph’s being a chain indicates that for every pair of jobs Ji and Jk in the subgraph, either Ji < Jk or Ji > Jk . Hence the jobs must be executed in serial order. In the subsequent chapters, we rarely use a task graph to describe a system of periodic tasks. You can see why from the above example: A list of periodic tasks and their parameters suffices. A graph such as the one in Figure 3–1 is necessary only when the system contains
components that have complex dependencies as exemplified by the subgraph below the periodic tasks.
Many types of interactions and communication among jobs are not captured by a precedence graph but can be captured by a task graph. Unlike a precedence graph, a task graph may contain different types of edges that represent different types of dependencies. The type(s) of dependency represented by an edge is given by the type(s) of the edge. The types of an edge connecting two vertices and other parameters of the edge are interconnection parameters of the jobs represented by the vertices.