Preemption-ceiling Protocol

PREEMPTION-CEILING PROTOCOL: We can avoid paying the time or storage overhead of the dynamic-priority-ceiling protocol described above for a class of dynamic-priority systems, which includes deadline-driven systems. We call systems in this class fixed preemption-level systems and will define this term shortly. For a fixed preemption-level system, Baker [Bake91] has a simpler approach to control resource accesses. The approach is based on the clever observation that the potentials of resource contentions in such a dynamic-priority system do not change with time, just as in fixed-priority systems, and hence can be analyzed statically.

The observation is supported by the following facts:

1. The fact that a job Jh has a higher priority than another job Jl and they both require some resource does not imply that Jl can directly block Jh. This blocking can occur only when it is possible for Jh to preempt Jl .
2. For some dynamic priority assignments, it is possible to determine a priori the possibility that jobs in each periodic task will preempt the jobs in other periodic tasks.

Because of fact 1, when determining whether a free resource can be granted to a job, it is not necessary to be concerned with the resource requirements of all higher-priority jobs; only those that can preempt the job. Fact 2 means that for some dynamic priority systems, the possibility that each periodic task will preempt every other periodic task does not change with time, just as in fixed-priority systems. We have already seen that in a deadline-driven system, no job in a periodic task with a smaller relative deadline is ever preempted by jobs in periodic tasks with identical or larger relative deadlines, despite the fact that some jobs in the latter may have higher priorities.

Preemption Levels ofJobs and Periodic Tasks
The possibility that a job Ji will preempt another job is captured by the parameter preemption level ψi of Ji . The preemption levels of jobs are functions of their priorities and release times. According to a valid preemption-level assignment, for every pair of jobs Ji and Jk , the preemption level ψi of Ji being equal to or higher than the preemption level ψk of Jk implies that it is never possible for Jk to preempt Ji . Stated in another way,

Validity Condition: If πi is higher than πk and ri > rk , then ψi is higher than ψk .

Given the priorities and release times of all jobs, this condition gives us a partial assignment of preemption levels, that is, the preemption levels of a subset of all jobs. The preemption levels of jobs that are not given by the above rule are valid as long as the linear order over all jobs defined by the preemption-level assignment does not violate the validity condition. As an example, we return to the system of jobs in Figure 8–8. Since jobs with higher priorities are released later, it is possible for every job to preempt all the jobs with lower priorities than itself. In this case, the preemption levels of the jobs dictated by the the validity condition give us a complete assignment. For these jobs, we can simply let the preemption levels of the jobs be equal to their respective priorities.

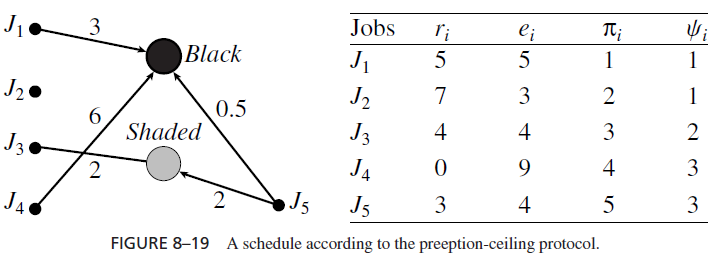
Figure 8–19 gives another example. As usual, the five jobs are indexed in decreasing priorities. Their release times are such that r4 < r5 < r3 < r1 < r2. We note that J1, the job with the highest priority, has a later release time than J3, J4, and J5. Hence, J1 should have a higher preemption level than these three jobs. However, it is never possible for J1 to preempt J2 because J1 has an earlier release time, and it is never possible for J2 to preempt J1, because J2 has a lower priority. We therefore give these two jobs the same preemption level. Similarly, J3 should have a higher preemption level than J4 and J5, and we can give J4 and J5 the same preemption level. In summary, we can assign ψi for i = 1, 2, 3, 4, and 5 the values 1, 1, 2, 3, and 3, respectively; it is easy see that this is a valid preemption level assignment. (Again, a smaller integer represents a higher preemption level.) Alternatively, we can assign preemption levels according to the release times of the jobs: the earlier the release time, the lower the preemption level. This assignment also satisfies the validity condition. The resultant preemption levels are 2, 1, 3, 5, and 4, respectively.

Let us now return to periodic tasks. When periodic tasks are scheduled on the EDF basis, a valid preemption-level assignment is according to the relative deadlines of jobs: the smaller the relative deadline, the higher the preemption level. (An assumption here is that

either release-time jitters are negligible or the relative deadlines of all jobs remain fixed despite release-time jitters.) For this preemption-level assignment, all the jobs in every periodic task in a deadline-driven system have the same preemption level. This is an example of fixed preemption-level systems. A system of periodic tasks is a fixed preemption-level system if there is a valid assignment of preemption levels to all jobs such that all the jobs in every task have the same preemption level. Clearly, all fixed-priority systems are also fixed preemptionlevel systems. Indeed, an obvious preemption-level assignment in a fixed-priority system is to make the preemption level of each job equal to its priority.

When there is no chance of confusion, we call the preemption level of all the jobs in a fixed preemption-level task Ti the preemption level of the task and denote it by ψi . We index periodic tasks in a fixed preemption-level system according to their preemption levels: the higher the level, the smaller the index. For example, suppose that the system of periodic tasks in Figure 8–16 are scheduled on the EDF basis. The preemption levels of the tasks T1, T2, T3,
and T4 are 1, 2, 3 and 4, respectively, because the relative deadlines of the tasks are 2, 2.2, 5, and 10, respectively.

In Priority-Driven Scheduling, we pointed out that when priorities are assigned on the FIFO basis or the LIFO basis, periodic tasks have dynamic priorities. In a FIFO system, no job is ever preempted. This is a degenerate fixed preemption-level system where all periodic tasks have the same preemption level. In contrast, periodic tasks scheduled on the LIFO basis have varying preemption levels. To illustrate, let us consider the system of three tasks T1, T2, and T3 in Figure 8–18. Suppose that the priorities of jobs in them are assigned on the LIFO basis. J1,1 is released later than J2,1 and J3,1, has a higher priority than they and hence can preempt these jobs. Also, J2,2 can preempt J1,2 and J3,1, and J3,2 can preempt J1,3 and J2,2. Suppose that we let the preemption level of each task at any time in a period equal the preemption level of the job released at the beginning of the period. For this system, we find that the preemption levels of the three tasks are 1, 2, and 3, respectively, in (0, 3); 2, 1, and 3 in (3, 4.5); 1, 2, and 3 in (4.5, 5); 2, 3, and 1 in (5, 6) and so on. In other words, this system has dynamic preemption levels.