Schedulability Of Deadline-driven Systems In The Presence Of Deferrable Server
Schedulability of Deadline-Driven Systems in the Presence of Deferrable Server: We now derive the schedulable utilization of a system of n independent periodic tasks that is scheduled according to the EDF algorithm together with a deferrable server of period ps and execution budget es. Let t be the deadline of a job Ji,c in some periodic task Ti and t−1 (< t ) be the latest time instant at which the processor is either idle or is executing a job whose deadline is after t .We observe that if Ji,c does not complete by t , the total amount wDS(t−t−1) of processor time consumed by the deferrable server in the interval (t−1, t ] is at most equal to

Figure 7–7 shows the condition under which the server consumes this amount of time.
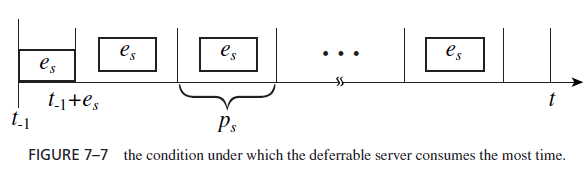
1. At time t−1, its budget is equal to es and the deadline for consuming the budget is (and hence the budget is to be replenished at) t−1 es .
2. One or more aperiodic jobs arrive at t−1, and the aperiodic job queue is never empty hereafter, at least until t .
3. The server’s deadline t−1 es is earlier than the deadlines of all the periodic jobs that are ready for execution in the interval (t−1, t−1 es ].
Under this condition, the server executes continuously in (t−1, t−1 es ]. If the current period (i.e., the period which begins before t and ends at or after t ) of the server also ends at t , the argument of the floor function in Eq. (7.3) is an integer; the floor function is equal to this integer. Otherwise, if the current period of the server ends after t , the server has a lowerpriority than Ji,c and is not given any time during this period. In either case, the total amount of the time consumed by the server after t−1 es is given by the second term in Eq. (7.3).
Since x ≤ x for all x ≥ 0 and us = es/ps , wDS(t − t−1) must satisfy the following inequality if the job Ji,c does not complete by its deadline at t :
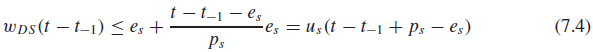
This observation leads to Theorem 7.3 [GhBa]. This theorem allows us to determine whether any periodic task Ti is schedulable when the periodic tasks are scheduled together with a deferrable server according to the EDF algorithm.
THEOREM . A periodic task Ti in a system of n independent, preemptive periodic tasks is schedulable with a deferrable server with period ps , execution budget es, and utilization us , according to the EDF algorithm if
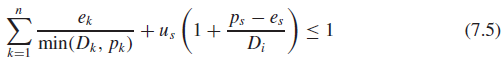
Proof. We suppose that a job misses its deadline at t and consider the interval (t−1, t ]. The interval begins at the latest time instant t−1 at which time the processor is either idle or is executing a job whose deadline is after t . The total amount of processor time used by each periodic task Tk in the time interval is bounded from above by ek(t − t−1)/pk . The fact that a job misses its deadline at t tells us that the total amount of time in this time interval used by all the periodic jobs with deadlines at or before t and the deferrable server exceeds the length of this interval. In other words,
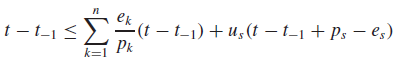
Dividing both sides of this inequality by t−t−1, we get Eq. (7.5) for the case of Dk ≥ pk .
As an example, let us consider again the system of three periodic tasks T1 = (3, 0.6), T2 = (5.0, 0.5), and T3 = (7, 1.4), which we studied earlier. The total utilization of the tasks is 0.5. If they are scheduled with a deferrable server whose period is 4 and execution time is 0.8, the values of the expression on the left-hand side of Eq. (7.5) for the three tasks are 0.913, 0.828 and 0.792, respectively. Hence, all three tasks are schedulable. From Eq. (7.5), we see that just as in a fixed-priority system, a deferrable server in a deadline-driven system behaves like a periodic task (ps , es) except that it may execute an extra amount of time in the feasible interval of any job. We treat this extra amount as the blocking time suffered by the job. In a fixed-priority system, the blocking time can be as large as es. In contrast, Theorem 7.3 says that the blocking caused by a deferrable server in a deadline-driven system is only (ps − es)us . (The latter is always less than the former. In our earlier example, es is 0.8, while (ps − es)us is only 0.64.)
We can take into account the effect of any number of deferrable servers in this way. (This corollary is stated as an exercise at the end of the chapter.) To illustrate, suppose that in addition to the server (4, 0.8) in the previous example, we have another deferrable server (2, 0.1) with utilization 0.05. The blocking time contributed by this server is 0.095. Adding the contribution of the second server to the left-hand side of (7.5) (i.e., adding 0.05 0.095/3.0 to 0.913), we get 0.995 for T1. Hence we can conclude that T1 remains to be schedulable. Similarly, T2 and T3 are schedulable.