Weighted Round-robin Approach

WEIGHTED ROUND-ROBIN APPROACH
The round-robin approach is commonly used for scheduling time-shared applications. When jobs are scheduled on a round-robin basis, every job joins a First-in-first-out (FIFO) queue when it becomes ready for execution. The job at the head of the queue executes for at most one time slice. (A time slice is the basic granule of time that is allocated to jobs. In a timeshared environment, a time slice is typically in the order of tens of milliseconds.) If the job does not complete by the end of the time slice, it is preempted and placed at the end of the queue to wait for its next turn. When there are n ready jobs in the queue, each job gets one time slice every n time slices, that is, every round. Because the length of the time slice is relatively short, the execution of every job begins almost immediately after it becomes ready. In essence, each job gets 1/nth share of the processor when there are n jobs ready for execution. This is why the round-robin algorithm is also called the processor-sharing algorithm.

The weighted round-robin algorithm has been used for scheduling real-time traffic in high-speed switched networks. It builds on the basic round-robin scheme. Rather than giving all the ready jobs equal shares of the processor, different jobs may be given different weights. Here, the weight of a job refers to the fraction of processor time allocated to the job. Specifically, a job with weight wt gets wt time slices every round, and the length of a round is equal to the sum of the weights of all the ready jobs. By adjusting the weights of jobs, we can speed up or retard the progress of each job toward its completion.

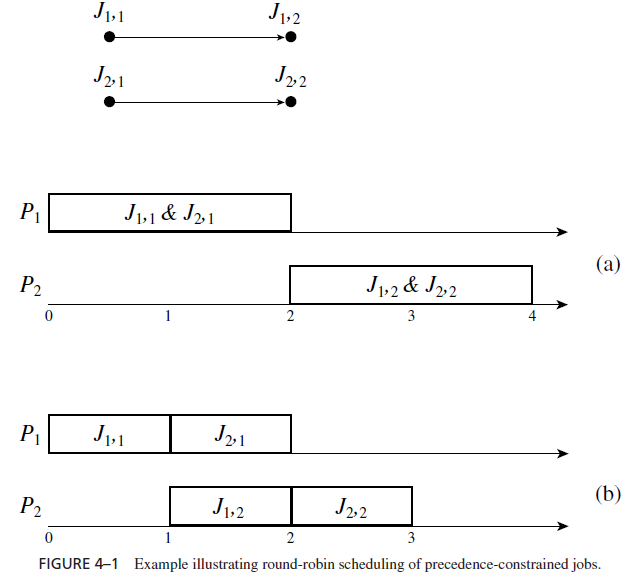
By giving each job a fraction of the processor, a round-robin scheduler delays the completion of every job. If it is used to schedule precedence constrained jobs, the response time of a chain of jobs can be unduly large. For this reason, the weighted round-robin approach is not suitable for scheduling such jobs. On the other hand, a successor job may be able to incrementally consume what is produced by a predecessor (e.g., as in the case of a UNIX pipe). In this case, weighted round-robin scheduling is a reasonable approach, since a job and its successors can execute concurrently in a pipelined fashion. As an example, we consider the two sets of jobs, J1 = {J1,1, J1,2} and J2 = {J2,1, J2,2}, shown in Figure 4–1. The release times of all jobs are 0, and their execution times are 1. J1,1 and J2,1 execute on processor P1, and J1,2 and J2,2 execute on processor P2. Suppose that J1,1 is the predecessor of J1,2, and J2,1 is the predecessor of J2,2. Figure 4–1(a) shows that both sets of jobs (i.e., the second jobs J1,2 and J2,2 in the sets) complete approximately at time 4 if the jobs are scheduled in a weighted round-robin manner. (We get this completion time when the length of the time slice is small compared with 1 and the jobs have the same weight.) In contrast, the schedule in Figure 4–1(b) shows that if the jobs on each processor are executed one after the other, one of the chains can complete at time 2, while the other can complete at time 3. On the other hand, suppose that the result of the first job in each set is piped to the second job in the set. The latter can execute after each one or a few time slices of the former complete. Then it is better to schedule the jobs on the round-robin basis because both sets can complete a few time slices after time 2.

Indeed, the transmission of each message is carried out by switches en route in a pipeline fashion. A switch downstream can begin to transmit an earlier portion of the message as soon as it receives the portion without having to wait for the arrival of the later portion of the message. The weighted round-robin approach does not require a sorted priority queue, only a round-robin queue. This is a distinct advantage for scheduling message transmissions in ultrahigh-speed networks, since priority queues with the required speed are expensive.