Case Study: The Rubber Machine
Introduction:
Design of experiments is the useful techniques for controlling statistical quality control and also it’s a much complicated techniques.it has a vital role in the field of optimization techniques. two additional case studies illustrate design of experiments (DOE) and regression being applied in real world manufacturing.
Case Study: the Rubber Machine (The Situation):
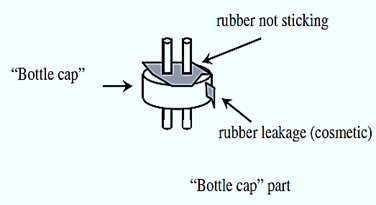
1. A Midwestern factory makes a small component used in air conditioning compressors for in-home applications, shown in Figure below. The company has established itself as the low cost leader in its sector and has maintained over 50%
2. of the world market for the type of component produced. For confidentiality reasons, we will refer to the part as a “bottle cap” which is the informal name sometimes used within the company.
3. In its desire to maintain momentum in cost-cutting and quality improvement, the company decided to purchase two new machines for applying rubber to the nickel-plated steel cap and hardening the rubber into place. The machines cost between $250,000 and $500,000 each in direct costs.
4. new machines required less labor content than the previous machines and promised to achieve the same results more consistently. Unfortunately, soon after the single production line was converted to using the new machine, the rubber stopped sticking on roughly 10% of the bottle caps produced. Because this failure type required expensive rework as well as 100% inspection and sorting, the company reverted to its old process.
Background Information:
a) A large fraction of the engineering and management resources of the small company were deployed as an initial team to fix the new machines.
b) During a period of roughly three months, engineer’s disrupted production in order to test their theories by running many units with one factor adjusted and then adjusting the settings back (one-factor-at-a-time, OFAT). Unfortunately, all of the tests results were inconclusive.
c) In addition, at least one polymer expert was flown in to inspect the problem and give opinions. Several months after the machines had been installed in the plant, the company was still unable to run them.
d) An additional series of OFAT experiments were conducted to investigate the effects of seven factors on the yields. Again, the results were inconclusive.
The Problem Statement:
Because of the unexpected need to use the old process, the company was rapidly losing money due to overtime and disruptions in the product flow through the plant. Therefore, the problem was to adjust the process inputs (x) to make the rubber stick onto the nickel plating consistently using the newer machines.
Unfortunately, the engineering and technicians had many theories about which factors should be adjusted to which levels, with little convincing evidence supporting the claims of each person (because of the application of OFAT). Seven candidate input factors were identified whose possible adjustment could solve the problem. Also, considering the volume of parts produced and the ease of inspection, it was possible to entertain the use of reasonably large batch sizes, i.e., b = 500 was possible.
Example(Rubber Machine Initial Results)
Which of the following could the first team most safely be accused of?
a. Leaders stifled creativity by adopting an overly formal decision making approach.
b. The team forfeited the ability to achieve statistical proof by using a nonrandom run order.
c. The team failed to apply engineering principles and relied too much on statistical methods.
d. The team failed to devote substantial resources to solve the problem.
Answer: This answer is virtually identical to the one in the printed circuit-board study. Compared with many of the methods described in this book, team one has adopted a fairly “organic” or creative decision style. Also, while it is usually
Possible to gain additional insights through recourse to engineering principles, it is likely that these principles were consulted in selecting factors for OFAT experimentation to a reasonable extent. In addition, the first team did provide
Enough data to determine the usual yields prior to implementing recommendations. Therefore, the criticisms in (a), (c), and (d) are probably not fair. According to , random run ordering is essential to establishing statistical proof.
Therefore, (b) is correct.