Continuous Random Variable
Introduction: Loosely speaking a random variable provides us with a numerical value, depending on the outcome of an experiment. More precisely, a random variable can be viewed as a function from the sample space to the real numbers, and we will use the notation X(ω) to denote the numerical value of a random variable X, when the outcome of the experiment is some particular ω.
Continuous random variables:
The definition of a continuous random variable is more subtle. It is not enough for a random variable to have a “continuous range.”

There is some ambiguity in the above definition, because the meaning of the integral of a measurable function may be unclear. For now, we just note that the integral is well-defined, and agrees with the Riemann integral encountered in calculus, if the function is continuous, or more generally, if it has a finite number of discontinuities.
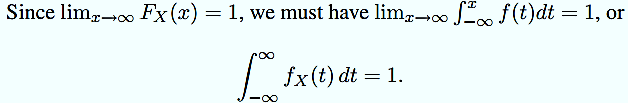
- Any non-negative measurable function that satisfies Eq. is called a density function. Conversely, given a density function f, we can define F(x) =xf(t) dt, −∞ and verify that F is a distribution function. It follows that given a density function, there always exists a random variable whose PDF is the given density.
-
If a CDF FX is differentiable at some x, the corresponding value fX(x) can be found by taking the derivative of FX at that point. However, CDFs need not be differentiable, so this will not always work. Let us also note that a PDF of a continuous random variable is not uniquely defined. We can always change the PDF at a finite set of points, without affecting its integral, hence multiple PDFs can be associated to the same CDF. However, this nonuniqueness rarely becomes an issue. In the sequel, we will often refer to “the PDF” of X, ignoring the fact that it is nonunique.