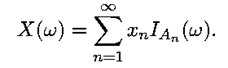Discrete Random Variables
Discrete random variables (cont.):
a) A random variable that takes only integer values is discrete. Also, every simple random variable is discrete, since it takes a finite number of values. However, more complicated discrete random variables are also possible.
b) Let the sample space be the set N of natural numbers, and consider a measure that satisfies P(n) = 1/2
c) n, for every n ∈N. The random variable X defined by X (n) = n is discrete.
d) Suppose now that the rational numbers have been arranged in a sequence, and that xn is the nth rational number, according to this sequence. Consider the random variable Y defined by Y (n) = xn. The range of this random variable is countable, so Y is a discrete random variable. Its range is the set of rational numbers, every rational number has positive probability, and the set of irrational numbers has zero probability. We close by noting that discrete random variables can be represented in terms of indicator functions. Indeed, given a discrete random variable X, with range {x1, x2, . . .},