Fundamental Probabilistic Models

Lévesque measure on [0, 1] and on r (cont.):

1.       We  start by  considering  the  sample  space Ω = (0, 1],  which  is  slightly  more  convenient  than  the  sample  space  [0, 1].

2.       2.1  A σ-field  and  a  field  of  subsets  of  (0, 1] Consider  the  collection  C of  all  intervals  [a, b] contained  in  (0, 1],  and  let  F be  the  σ-field  generated  by  C. 

a.       Sets  in  this  σ-field  are  called  Borel  sets  or  Borel  measurable  sets.  Any set  that  can be  formed by starting  with  intervals  [a, b] and  using a  count­able  number  of  set-theoretic  operations  (taking  complements,  or  forming  count­ able unions and  intersections of previously formed sets) is a Borel set. For example,  it  can  be  verified  that  single-element  sets,  {a},  are  Borel  sets.  Furthermore,  intervals  (a, b] are  also  Borel  sets  since  they  are  of  the  form  [a, b] \ {a}.  Every

b.      countable  set  is  also  a  Borel  set,  since  it  is  the  union  of  countably  many single­ element  sets.  In  particular,  the  set  of  rational  numbers  in  (0, 1],  as  well  as  its  complement,  the  set  of  irrational  numbers  in  (0, 1],  is  a  Borel  set.  While  Borel  sets  can be fairly  complicated,  not every  set is a  Borel  set;  see  Sections  5-6.  Directly  defining a  probability  measure for all  Borel  sets  directly is difficult,  so  we  start  by  considering  a  smaller  collection,  F0,  of  subsets  of  (0, 1].  We  let  F₀ consist  of  the  empty  set  and  all  sets  that  are  finite  unions  of  intervals  of  the  form  (a, b].  In  more  detail,  if  a  set  A ∈F₀ is  nonempty,  it  is  of  the  form

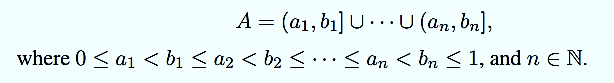
Lemma 1.  We have σ (F₀) = σ(C) = B.

Proof.  We  have  already  argued  that  every  interval  of  the  form (a, b] is  a  Borel  set.  Hence,  a  typical  element  of  F0 (a  finite  union  of  such  intervals)  is  also  a Borel  set.  Therefore, F₀ ⊂B, which implies that σ (F₀) ⊂σ (B) = B.  (The  last  equality  holds  because  B is  already  a  σ-field  and  is  therefore  equal  to  the  smallest  σ-field  that  contains  B.)  Note that for a > 0, (a−1/n, b].  Since (a−1/n, b] ∈

F₀ ⊂σ (F₀), it follows that [a, b] ∈σ (F₀).  Thus, C ⊂σ (F₀), which implies that

B = σ(C) ⊂σ (F₀) = σ (F₀) ⊂B.

The first equality in the statement of the proposition follows.  Finally, the equality σ(C) = B is just the definition of B.

Lemma 2.

(a)  The collection F₀ is a field.

(b)  The collection F₀ is not an σ-field.

Proof.

(a)  By definition, Ø ∈F0.  Note that Ø_c= (0, 1] ∈F₀.  More  generally,  if  A is  of  the  form  A = (a₁, b₁]∪···∪(a_n, b_n], its  complement  is (0, a₁]∪(b₁, a₂]∪· · · ∪(b_n, 1],  which  is  also  in  F0.  Furthermore,  the  union  of  two  sets  that  are  unions  of  finitely  many  intervals  of  the  form  (a, b] is  also  a  union  of  finitely  many such  intervals.  For example, if  A = (1/8, 2/8] ∪(4/8, 7/8] and  B = (3/8, 5/8],  then  A ∪B = (1/8, 2/8] ∪(3/8, 7/8].

(b)  To  see  that  F0 is  not a  σ-field,  note  that  (0, n/(n 1)] ∈F₀,  for  every  n ∈N,  but  the  union  of  these  sets,  which  is  (0, 1),  does  not  belong  to F₀.