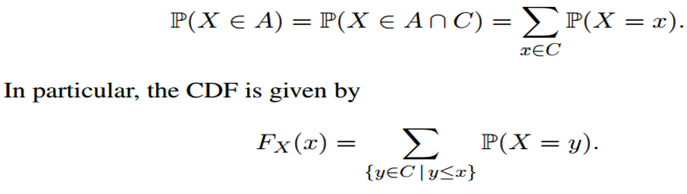The Law Of Random Variable

The  law of a  random variable: “For a random variable X, the event {ω | X(ω) ≤ c} is  often  written  as  {X ≤ c},  and is  sometimes just  called “the event that  X ≤ c.” The  probability of this event  is  well  defined,  since  this  event  belongs  to  F.  Let  now  B be  a  more  general

subset  of  the  real  line.  We  use  the  notation  X−1(B) or  {X ∈B} to  denote  the  set  {ω | X(ω) ∈B}”

• Because  the  collection  of  intervals  of  the  form  (−∞, c] generates  the  Borel  σ-field  in  R,  it  can  be  shown  that  if  X is  a  random  variable,  then  for  any  Borel  set  B,  the  set  X−1
• (B) is  F-measurable.  It  follows  that  the  probability  P X−1
• (B) = P({ω | X(ω) ∈B}) is  well-defined.  It  is  often  denoted  by  P(X ∈B).
• Sometimes,  P_X is  also  called  the  distribution  of  X,  not  to  be  confused  with the  cumulative  distribution  function  defined  in  the  next  section. According  to  the  next  result,  the  law  P_X of  X is  also  a  probability  measure. Notice  here  that  P_X is  a  measure  on  (R, B),  as  opposed  to  the  original  measure P,  which  is  a  measure  on  (Ω, F).
• In  many  instances,  the  original  probability space  (Ω, F, P) remains  in  the  background,  hidden  or  unused,  and  one  works directly  with  the  much  more  tangible  probability  space  (R, B, P_X).  Indeed,  if we  are  only  interested  in  the  statistical  properties  of  the  random  variable  X,  the latter  space  will  do.\

Proof:  Clearly,  PX(B) ≥ 0,  for  every  Borel  set  B.  Also,  PX(R) = P(X ∈R) = P(Ω) = 1.  We  now  verify  countable  additivity.  Let  {Bi} be  a  countable sequence  of  disjoint  Borel  subsets  of  R.  Note  that  the  sets  X−1(Bi) are  also disjoint,  and  that

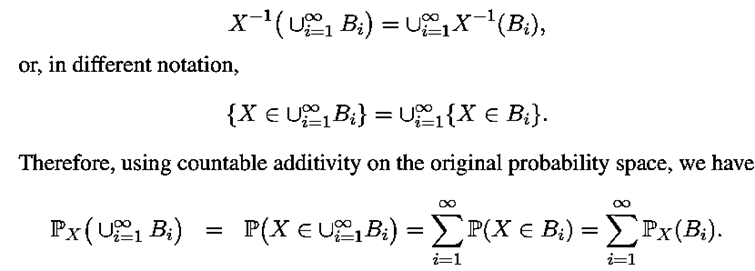
 Discrete  random variables:

Discrete random  variables  take  values  in  a  countable  set.  We  need  some  nota­tion.  Given  a  function  f : Ω → R,  its  range  is  the  set f(Ω) = {x ∈R | ∃ω∈Ωsuch  that  f(ω) = x}. Discrete  random  variables  and  PMFs)

(a)A random variable  X,  defined  on a  probability  space (Ω, F, P),  is  said  to  be discrete  if  its  range  X(Ω) is  countable.

(b)  If  X is  a  discrete  random  variable,  the  function  p_X : R → [0, 1] defined by p_X(x) = P(X = x),  for  every  x,  is  called  the  (probability)  mass  function of  X,  or  PMF  for  short. Consider  a  discrete  random  variable  X whose  range  is  a  finite  set  C.  In  that case,  for  any Borel  set  A,  countable  additivity  yields