Types Of Pmf

 Joint, marginal, and conditional pmfs: In  most  applications,  one  typically  deals  with  several  random  variables  at  once. 

a.      Marginal PMFs:

Consider  two  discrete  random  variables  X and  Y associated  with  the  same  ex­periment.  The  probability  law  of  each  one  of  them  is  described  by  the  corre­sponding  PMF,  pX or  pY ,  called a marginal  PMF.  However, the  marginal  PMFs do  not  provide  any information  on  possible  relations  between  these  two  random variables.  For  example,  suppose  that  the  PMF  of  X is  symmetric  around  the origin.  If  we  have  either  Y = X or  Y = −X,  the  PMF  of  Y remains  the  same, and fails to  capture the  specifics of the  dependence  between  X and  Y .

b.      Joint  PMFs :

The  statistical  properties  of  two  random  variables  X and  Y are  captured  by  a  function  x,y : R2 → [0, 1],  defined  by

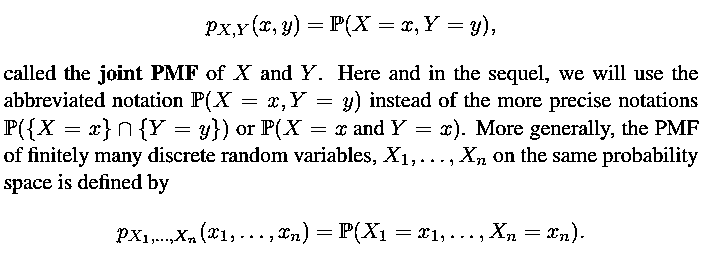
The  joint  PMF  of  X and  Y determines  the  probability  of  any  event  that  can be  specified  in  terms  of  the  random  variables  X and  Y . For example if  A is  the set  of  all  pairs  (x, y) that  have  a  certain  property,  then

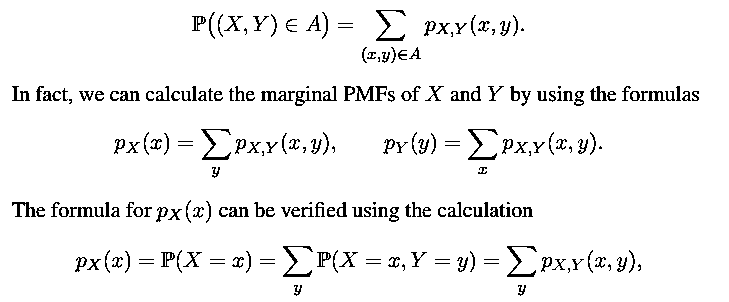
where  the  second  equality  follows by noting  that  the event  {X = x} is  the  union of  the  countably  many disjoint  events  {X = x, Y = y},  as  y ranges  over  all  the different values of  Y .  The formula for pY (y) is verified similarly.