1. In simple motion, every strait line taken in the body moved is so carried, that it is always parallel to the places in which it formerly was.—2. If circular motion be made about a resting centre, and in that circle there be an epicycle, whose revolution is made the contrary way, in such manner that in equal times it make equal angles, every strait line taken in that epicycle will be so carried, that it will always be parallel to the places in which it formerly was.—3. The properties of simple motion.—4. If a fluid be moved with simple circular motion, all the points taken in it will describe their circles in times proportional to the distances from the centre.—5. Simple motion dissipates heterogeneous and congregates homogeneous bodies.—6. If a circle made by a movent moved with simple motion be commensurable to another circle made by a point which is carried about by the same movent, all the points of both the circles will at some time return to the same situation.—7.. If a sphere have simple motion, its motion will more dissipate heterogeneous bodies by how much it is more remote from the poles.—8. If the simple circular motion of a fluid body be hindered by a body which is not fluid, the fluid body will spread itself upon the superficies of that body.—9. Circular motion about a fixed centre casteth off by the tangent such things as lie upon the circumference and stick not to it.—10. Such things, as are moved with simple circular motion, beget simple circular motion.—11. If that which is so moved have one side hard and the other side fluid, its motion will not be perfectly circular.

1. I have already defined simple motion to be that, in which the several points taken in a moved body do in several equal times describe several equal arches. And therefore in simple circular motion it is necessary that every strait line taken in the moved body be always carried parallel to itself; which I thus demonstrate.

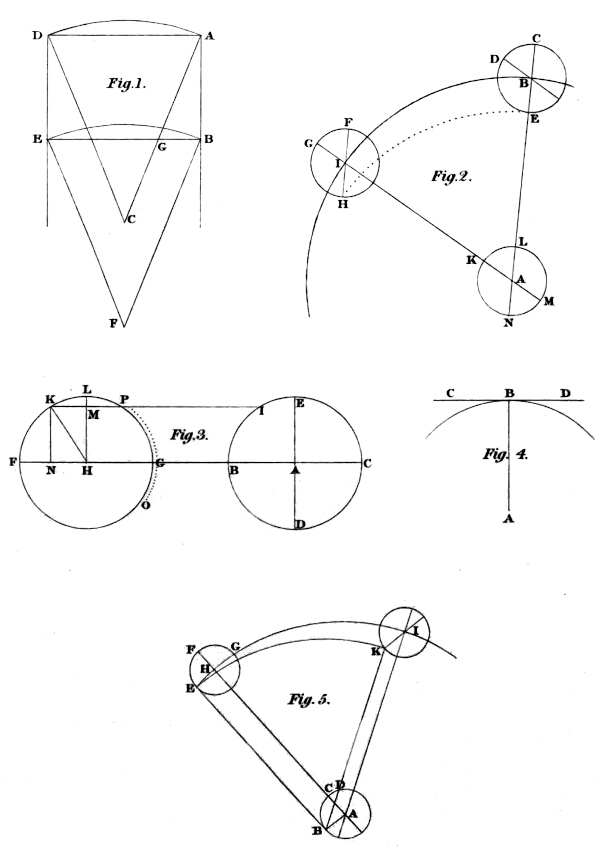
First, let A B (in the first figure) be any strait line taken in any solid body; and let A D be any arch drawn upon any centre C and radius CA. Let the point B be understood to describe towards the same parts the arch B E, like and equal to the arch A D. Now in the same time in which the point A transmits the arch A D, the point B, which by reason of its simple motion is supposed to be carried with a velocity equal to that of A, will transmit the arch B E; and at the end of the same time the whole A B will be in D E; and therefore A B and D E are equal. And seeing the arches A D and B E are like and equal, their subtending strait lines AD and BE will also be equal; and therefore the four-sided figure A B D E will be a parallelogram. Wherefore A B is carried parallel to itself. And the same may be proved by the same method, if any other strait line be taken in the same moved body in which the strait line A B was taken. So that all strait lines, taken in a body moved with simple circular motion, will be carried parallel to themselves.

Coroll. I. It is manifest that the same will also happen in any body which hath simple motion, though not circular. For all the points of any strait line whatsoever will describe lines, though not circular, yet equal; so that though the crooked lines A D and B E were not arches of circles, but of parabolas, ellipses, or of any other figures, yet both they, and their subtenses, and the strait lines which join them, would be equal and parallel.

Coroll. II. It is also manifest, that the radii of the equal circles A D and B E, or the axis of a sphere, will be so carried, as to be always parallel to the places in which they formerly were. For the strait line B F drawn to the centre of the arch B E being equal to the radius A C, will also be equal to the strait line F E or C D; and the angle B F E will be equal to the angle A C D. Now the intersection of the strait lines C A and B E being at G, the angle C G E (seeing B E and A D are parallel) will be equal to the angle D A C. But the angle E B F is equal to the same angle D A C; and therefore the angles C G E and E B F are also equal. Wherefore A C and B F are parallel; which was to be demonstrated.

2. Let there be a circle given (in the second figure) whose centre is A, and radius A B; and upon the centre B and any radius B C let the epicycle C D E be described. Let the centre B be understood to be carried about the centre A, and the whole epicycle with it till it be coincident with the circle F G H, whose centre is I; and let B A I be any angle given. But in the time that the centre B is moved to I, let the epicycle C D E have a contrary revolution upon its own centre, namely from E by D to C, according to the same proportions; that is, in such manner, that in both the circles, equal angles be made in equal times. I say E C, the axis of the epicycle, will be always carried parallel to itself. Let the angle F I G be made equal to the angle B A I; I F and A B will therefore be parallel; and how much the axis A G has departed from its former place A C (the measure of which progression is the angle C A G, or C B D, which I suppose equal to it) so much in the same time has the axis I G, the same with B C, departed from its own former situation. Wherefore, in what time B C comes to I G by the motion from B to I upon the centre A, in the same time G will come to F by the contrary motion of the epicycle; that is, it will be turned backwards to F, and I G will lie in I F. But the angles F I G and G A C are equal; and therefore A C, that is, B C, and I F, (that is the axis, though in different places) will be parallel. Wherefore, the axis of the epicycle E D C will be carried always parallel to itself; which was to be proved.

Coroll. From hence it is manifest, that those two annual motions which Copernicus ascribes to the earth, are reducible to this one circular simple motion, by which all the points of the moved body are carried always with equal velocity, that is, in equal times they make equal revolutions uniformly.

This, as it is the most simple, so it is the most frequent of all circular motions; being the same which is used by all men when they turn anything round with their arms, as they do in grinding or sifting. For all the points of the thing moved describe lines which are like and equal to one another. So that if a man had a ruler, in which many pens' points of equal length were fastened, he might with this one motion write many lines at once.

3. Having shown what simple motion is, I will here also set down some properties of the same.

First, when a body is moved with simple motion in a fluid medium which hath no vacuity, it changes the situation of all the parts of the fluid ambient which resist its motion; I say there are no parts so small of the fluid ambient, how far soever it be continued, but do change their situation in such manner, as that they leave their places continually to other small parts that come into the same.

For (in the same second figure) let any body, as K L M N, be understood to be moved with simple circular motion; and let the circle, which every point thereof describes, have any determined quantity, suppose that of the same K L M N. Wherefore the centre A and every other point, and consequently the moved body itself, will be carried sometimes towards the side where is K, and sometimes towards the other side where is M. When therefore it is carried to K, the parts of the fluid medium on that side will go back; and, supposing all space to be full, others on the other side will succeed. And so it will be when the body is carried to the side M, and to N, and every way. Now when the nearest parts of the fluid medium go back, it is necessary that the parts next to those nearest parts go back also; and supposing still all space to be full, other parts will come into their places with succession perpetual and infinite. Wherefore all, even the least parts of the fluid medium, change their places, &c. Which was to be proved.

It is evident from hence, that simple motion, whether circular or not circular, of bodies which make perpetual returns to their former places, hath greater or less force to dissipate the parts of resisting bodies, as it is more or less swift, and as the lines described have greater or less magnitude. Now the greatest velocity that can be, may be understood to be in the least circuit, and the least in the greatest; and may be so supposed, when there is need.

4. Secondly, supposing the same simple motion in the air, water, or other fluid medium; the parts of the medium, which adhere to the moved body, will be carried about with the same motion and velocity, so that in what time soever any point of the movent finishes its circle, in the same time every part of the medium, which adheres to the movent, shall also describe such a part of its circle, as is equal to the whole circle of the movent; I say, it shall describe a part, and not the whole circle, because all its parts receive their motion from an interior concentric movent, and of concentric circles the exterior are always greater than the interior; nor can the motion imprinted by any movent be of greater velocity than that of the movent itself. From whence it follows, that the more remote parts of the fluid ambient shall finish their circles in times, which have to one another the same proportion with their distances from the movent. For every point of the fluid ambient, as long as it toucheth the body which carries it about, is carried about with it, and would make the same circle, but that it is left behind so much as the exterior circle exceeds the interior. So that if we suppose some thing, which is not fluid, to float in that part of the fluid ambient which is nearest to the movent, it will together with the movent be carried about. Now that part of the fluid ambient, which is not the nearest but almost the nearest, receiving its degree of velocity from the nearest, which degree cannot be greater than it was in the giver, doth therefore in the same time make a circular line, not a whole circle, yet equal to the whole circle of the nearest. Therefore in the same time that the movent describes its circle, that which doth not touch it shall not describe its circle; yet it shall describe such a part of it, as is equal to the whole circle of the movent. And after the same manner, the more remote parts of the ambient will describe in the same time such parts of their circles, as shall be severally equal to the whole circle of the movent; and, by consequent, they shall finish their whole circles in times proportional to their distances from the movent; which was to be proved.

5. Thirdly, the same simple motion of a body placed in a fluid medium, congregates or gathers into one place such things as naturally float in that medium, if they be homogeneous; and if they be heterogeneous, it separates and dissipates them. But if such things as be heterogeneous do not float, but settle, then the same motion stirs and mingles them disorderly together. For seeing bodies, which are unlike to one another, that is, heterogeneous bodies, are not unlike in that they are bodies; for bodies, as bodies, have no difference; but only from some special cause, that is, from some internal motion, or motions of their smallest parts (for I have shown in chap. IX, art. 9, that all mutation is such motion), it remains that heterogeneous bodies have their unlikeness or difference from one another from their internal or specifical motions. Now bodies which have such difference receive unlike and different motions from the same external common movent; and therefore they will not be moved together, that is to say, they will be dissipated. And being dissipated they will necessarily at some time or other meet with bodies like themselves, and be moved alike and together with them; and afterwards meeting with more bodies like themselves, they will unite and become greater bodies. Wherefore homogeneous bodies are congregated, and heterogeneous dissipated by simple motion in a medium where they naturally float. Again, such as being in a fluid medium do not float, but sink, if the motion of the fluid medium be strong enough, will be stirred up and carried away by that motion, and consequently they will be hindered from returning to that place to which they sink naturally, and in which only they would unite, and out of which they are promiscuously carried; that is, they are disorderly mingled.

Now this motion, by which homogeneous bodies are congregated and heterogeneous are scattered, is that which is commonly called fermentation, from the Latin fervere; as the Greeks have their Ζύμη, which signifies the same, from Ζέω ferveo. For seething makes all the parts of the water change their places; and the parts of any thing, that is thrown into it, will go several ways according to their several natures. And yet all fervour or seething is not caused by fire; for new wine and many other things have also their fermentation and fervour, to which fire contributes little, and sometimes nothing. But when in fermentation we find heat, it is made by the fermentation.

6. Fourthly, in what time soever the movent, whose centre is A (in fig. 2) moved in K L N, shall, by any number of revolutions, that is, when the perimeters B I and K L N be commensurable, have described a line equal to the circle which passes through the points B and I; in the same time all the points of the floating body, whose centre is B, shall return to have the same situation in respect of the movent, from which they departed. For seeing it is as the distance B A, that is, as the radius of the circle which passes through B I is to the perimeter itself B I, so the radius of the circle K L N is to the perimeter K L N; and seeing the velocities of the points B and K are equal, the time also of the revolution in I B to the time of one revolution in K L N, will be as the perimeter B I to the perimeter K L N; and therefore so many revolutions in K L N, as together taken are equal to the perimeter B I, will be finished in the same time in which the whole perimeter B I is finished; and therefore also the points L, N, F and H, or any of the rest, will in the same time return to the same situation from which they departed; and this may be demonstrated, whatsoever be the points considered. Wherefore all the points shall in that time return to the same situation; which was to be proved.

From hence it follows, that if the perimeters B I and L K N be not commensurable, then all the points will never return to have the same situation or configuration in respect of one another.

7. In simple motion, if the body moved be of a spherical figure, it hath less force towards its poles than towards its middle to dissipate heterogeneous, or to congregate homogeneous bodies.

Let there be a sphere (as in the third figure) whose centre is A and diameter B C; and let it be conceived to be moved with simple circular motion; of which motion let the axis be the strait line D E, cutting the diameter B C at right angles in A. Let now the circle, which is described by any point B of the sphere, have B F for its diameter; and taking F G equal to B C, and dividing it in the middle in H, the centre of the sphere A will, when half a revolution is finished, lie in H. And seeing H F and A B are equal, a circle described upon the centre H with the radius H F or H G, will be equal to the circle whose centre is A and radius A B. And if the same motion be continued, the point B will at the end of another half revolution return to the place from whence it began to be moved; and therefore at the end of half a revolution, the point B will be carried to F, and the whole hemisphere D B E into that hemisphere in which are the points L, K and F. Wherefore that part of the fluid medium, which is contiguous to the point F, will in the same time go back the length of the strait line B F; and in the return of the point F to B, that is, of G to C, the fluid medium will go back as much in a strait line from the point C. And this is the effect of simple motion in the middle of the sphere, where the distance from the poles is greatest. Let now the point I be taken in the same sphere nearer to the pole E, and through it let the strait line I K be drawn parallel to the strait line B F, cutting the arch F L in K, and the axis H L in M; then connecting H K, upon H F let the perpendicular K N be drawn. In the same time therefore that B comes to F the point I will come to K, B F and I K being equal and described with the same velocity. Now the motion in I K to the fluid medium upon which it works, namely, to that part of the medium which is contiguous to the point K, is oblique, whereas if it proceeded in the strait line H K it would be perpendicular; and therefore the motion which proceeds in I K has less power than that which proceeds in H K with the same velocity. But the motions in H K and H F do equally thrust back the medium; and therefore the part of the sphere at K moves the medium less than the part at F, namely, so much less as K N is less than H F. Wherefore also the same motion hath less power to disperse heterogeneous, and to congregate homogeneous bodies, when it is nearer, than when it is more remote from the poles; which was to be proved.

Coroll. It is also necessary, that in planes which are perpendicular to the axis, and more remote than the pole itself from the middle of the sphere, this simple motion have no effect. For the axis D E with simple motion describes the superficies of a cylinder; and towards the bases of the cylinder there is in this motion no endeavour at all.

8. If in a fluid medium moved about, as hath been said, with simple motion, there be conceived to float some other spherical body which is not fluid, the parts of the medium, which are stopped by that body, will endeavour to spread themselves every way upon the superficies of it. And this is manifest enough by experience, namely, by the spreading of water poured out upon a pavement. But the reason of it may be this. Seeing the sphere A (in fig. 3) is moved towards B, the medium also in which it is moved will have the same motion. But because in this motion it falls upon a body not liquid, as G, so that it cannot go on; and seeing the small parts of the medium cannot go forwards, nor can they go directly backwards against the force of the movent; it remains, therefore, that they diffuse themselves upon the superficies of that body, as towards O and P; which was to be proved.

9. Compounded circular motion, in which all the parts of the moved body do at once describe circumferences, some greater, others less, according to the proportion of their several distances from the common centre, carries about with it such bodies, as being not fluid, adhere to the body so moved; and such as do not adhere, it casteth forwards in a strait line which is a tangent to the point from which they are cast off.

For let there be a circle whose radius is A B (in fig. 4); and let a body be placed in the circumference in B, which if it be fixed there, will necessarily be carried about with it, as is manifest of itself. But whilst the motion proceeds, let us suppose that body to be unfixed in B. I say, the body will continue its motion in the tangent B C. For let both the radius A B and the sphere B be conceived to consist of hard matter; and let us suppose the radius A B to be stricken in the point B by some other body which falls upon it in the tangent D B. Now, therefore, there will be a motion made by the concourse of two things, the one, endeavour towards C in the strait line D B produced, in which the body B would proceed, if it were not retained by the radius A B; the other, the retention itself. But the retention alone causeth no endeavour towards the centre; and, therefore, the retention being taken away, which is done by the unfixing of B, there will remain but one endeavour in B, namely, that in the tangent B C. Wherefore the motion of the body B unfixed will proceed in the tangent B C; which was to be proved.

By this demonstration it is manifest, that circular motion about an unmoved axis shakes off and puts further from the centre of its motion such things as touch, but do not stick fast to its superficies; and the more, by how much the distance is greater from the poles of the circular motion; and so much the more also, by how much the things, that are shaken off, are less driven towards the centre by the fluid ambient, for other causes.

10. If in a fluid medium a spherical body be moved with simple circular motion, and in the same medium there float another sphere whose matter is not fluid, this sphere also shall be moved with simple circular motion.

Let B C D (in fig. 5) be a circle, whose centre is A, and in whose circumference there is a sphere so moved, that it describes with simple motion thethe perimeter B C D. Let also E F G be another sphere of consistent matter, whose semidiameter is E H, and centre H; and with the radius A H let the circle H I be described. I say, the sphere E F G will, by the motion of the body in B C D, be moved in the circumference H I with simple motion.

For seeing the motion in B C D (by art. 4 of this chapter) makes all the points of the fluid medium describe in the same time circular lines equal to one another, the points E, H and G of the strait line E H G will in the same time describe with equal radii equal circles. Let E B be drawn equal and parallel to the strait line A H; and let A B be connected, which will therefore be equal and parallel to E H; and therefore also, if upon the centre B and radius B E the arch E K be drawn equal to the arch H I, and the strait lines A I, B K and I K be drawn, B K and A I will be equal; and they will also be parallel, because the two arches E K and H I, that is, the two angles K B E and I A H are equal; and, consequently, the strait lines A B and K I, which connect them, will also be equal and parallel. Wherefore K I and E H are parallel. Seeing, therefore, E and H are carried in the same time to K and I, the whole strait line I K will be parallel to E H, from whence it departed. And, therefore, seeing the sphere E F G is supposed to be of consistent matter, so as all its points keep always the same situation, it is necessary that every other strait line, taken in the same sphere, be carried always parallel to the places in which it formerly was. Wherefore the sphere E F G is moved with simple circular motion; which was to be demonstrated.

11. If in a fluid medium, whose parts are stirred by a body moved with simple motion, there float another body, which hath its superficies either wholly hard, or wholly fluid, the parts of this body shall approach the centre equally on all sides; that is to say, the motion of the body shall be circular, and concentric with the motion of the movent. But if it have one side hard, and the other side fluid, then both those motions shall not have the same centre, nor shall the floating body be moved in the circumference of a perfect circle.

Let a body be moved in the circumference of the circle K L M N (in fig 2.) whose centre is A. And let there be another body at I, whose superficies is either all hard or all fluid. Also let the medium, in which both these bodies are placed, be fluid. I say, the body at I will be moved in the circle I B about the centre A. For this has been demonstrated in the last article.

Wherefore let the superficies of the body at I be fluid on one side, and hard on the other. And first, let the fluid side be towards the centre. Seeing, therefore, the motion of the medium is such, as that its parts do continually change their places, (as hath been shown in art 5); if this change of place be considered in those parts of the medium which are contiguous to the fluid superficies, it must needs be that the small parts of that superficies enter into the places of the small parts of the medium which are contiguous to them; and the like change of place will be made with the next contiguous parts towards A. And if the fluid parts of the body at I have any degree at all of tenacity (for there are degrees of tenacity, as in the air and water) the whole fluid side will be lifted up a little, but so much the less, as its parts have less tenacity; whereas the hard part of the superficies, which is contiguous to the fluid part, has no cause at all of elevation, that is to say, no endeavour towards A.

Secondly, let the hard superficies of the body at I be towards A. By reason, therefore, of the said change of place of the parts which are contiguous to it, the hard superficies must, of necessity, seeing by supposition there is no empty space, either come nearer to A, or else its smallest parts must supply the contiguous places of the medium, which otherwise would be empty. But this cannot be, by reason of the supposed hardness; and, therefore, the other must needs be, namely, that the body come nearer to A. Wherefore the body at I has greater endeavour towards the centre A, when its hard side is next it, than when it is averted from it. But the body in I, while it is moving in the circumference of the circle I B, has sometimes one side, sometimes another, turned towards the centre; and, therefore, it is sometimes nearer, sometimes further off from the centre A. Wherefore the body at I is not carried in the circumference of a perfect circle; which was to be demonstrated.

Vol. 1. Lat. & Eng.
C. XXI.
Fig. 1-5

CHAPTER XXII.

OF OTHER VARIETY OF MOTION.

1. Endeavour and pressure how they differ.—2. Two kinds of mediums in which bodies are moved.—3. Propagation of motion, what it is.—4. What motion bodies have, when they press one another.—5. Fluid bodies, when they are pressed together, penetrate one another.—6. When one body presseth another and doth not penetrate it, the action of the pressing body is perpendicular to the superficies of the body pressed.—7. When a hard body, pressing another body, penetrates the same, it doth not penetrate it perpendicularly, unless it fall perpendicularly upon it.—8. Motion sometimes opposite to that of the movent.—9. In a full medium, motion is propagated to any distance.—10. Dilatation and contraction what they are.—11. Dilatation and contraction suppose mutation of the smallest parts in respect of their situation.—12. All traction is pulsion.—13. Such things as being pressed or bent restore themselves, have motion in their internal parts.—14. Though that which carrieth another be stopped, the body carried will proceed.—15, 16. The effects of percussion not to be compared with those of weight.—17, 18. Motion cannot begin first in the internal parts of a body.—19. Action and reaction proceed in the same line.—20. Habit, what it is.

1. I have already (chapter XV. art. 2) defined endeavour to be motion through some length, though not considered as length, but as a point. Whether, therefore, there be resistance or no resistance, the endeavour will still be the same. For simply to endeavour is to go. But when two bodies, having opposite endeavours, press one another, then the endeavour of either of them is that which we call pressure, and is mutual when their pressures are opposite.

2. Bodies moved, and also the mediums in which they are moved, are of two kinds. For either they have their parts coherent in such manner, as no part of the moved body will easily yield to the movent, except the whole body yield also, and such are the things we call hard: or else their parts, while the whole remains unmoved, will easily yield to the movent, and these we call fluid or soft bodies. For the words fluid, soft, tough, and hard, in the same manner as great and little, are used only comparatively; and are not different kinds, but different degrees of quality.

3. To do, and to suffer, is to move and to be moved; and nothing is moved but by that which toucheth it and is also moved, as has been formerly shown. And how great soever the distance be, we say the first movent moveth the last moved body, but mediately; namely so, as that the first moveth the second, the second the third, and so on, till the last of all be touched. When therefore one body, having opposite endeavour to another body, moveth the same, and that moveth a third, and so on, I call that action propagation of motion.

4. When two fluid bodies, which are in a free and open space, press one another, their parts will endeavour, or be moved, towards the sides; not only those parts which are there where the mutual contact is, but all the other parts. For in the first contact, the parts, which are pressed by both the endeavouring bodies, have no place either forwards or backwards in which they can be moved; and therefore they are pressed out towards the sides. And this expressure, when the forces are equal, is in a line perpendicular to the bodies pressing. But whensoever the foremost parts of both the bodies are pressed, the hindermost also must be pressed at the same time; for the motion of the hindermost parts cannot in an instant be stopped by the resistance of the foremost parts, but proceeds for some time; and therefore, seeing they must have some place in which they may be moved, and that there is no place at all for them forwards, it is necessary that they be moved into the places which are towards the sides every way. And this effect follows of necessity, not only in fluid, but in consistent and hard bodies, though it be not always manifest to sense. For though from the compression of two stones we cannot with our eyes discern any swelling outwards towards the sides, as we perceive in two bodies of wax; yet we know well enough by reason, that some tumour must needs be there, though it be but little.

5. But when the space is enclosed, and both the bodies be fluid, they will, if they be pressed together, penetrate one another, though differently, according to their different endeavours. For suppose a hollow cylinder of hard matter, well stopped at both ends, but filled first, below with some heavy fluid body, as quicksilver, and above with water or air. If now the bottom of the cylinder be turned upwards, the heaviest fluid body, which is now at the top, having the greatest endeavour downwards, and being by the hard sides of the vessel hindered from extending itself sideways, must of necessity either be received by the lighter body, that it may sink through it, or else it must open a passage through itself, by which the lighter body may ascend. For of the two bodies, that, whose parts are most easily separated, will be the first divided; which being done, it is not necessary that the parts of the other suffer any separation at all. And therefore when two liquors, which are enclosed in the same vessel, change their places, there is no need that their smallest parts should be mingled with one another; for a way being opened through one of them, the parts of the other need not be separated.

Now if a fluid body, which is not enclosed, press a hard body, its endeavour will indeed be towards the internal parts of that hard body; but being excluded by the resistance of it, the parts of the fluid body will be moved every way according to the superficies of the hard body, and that equally, if the pressure be perpendicular; for when all the parts of the cause are equal, the effects will be equal also. But if the pressure be not perpendicular, then the angles of the incidence being unequal, the expansion also will be unequal, namely, greater on that side where the angle is greater, because that motion is most direct which proceeds by the directest line.

6. If a body, pressing another body, do not penetrate it, it will nevertheless give to the part it presseth an endeavour to yield, and recede in a strait line perpendicular to its superficies in that point in which it is pressed.

Let A B C D (in fig. 1) be a hard body, and let another body, falling upon it in the strait line E A, with any inclination or without inclination, press it in the point A. I say the body so pressing, and not penetrating it, will give to the part A an endeavour to yield or recede in a strait line perpendicular to the line A D.

For let A B be perpendicular to A D, and let B A be produced to F. If therefore A F be coincident with A E, it is of itself manifest that the motion in E A will make A to endeavour in the line A B. Let now E A be oblique to A D, and from the point E let the strait line E C be drawn, cutting A D at right angles in D, and let the rectangles A B C D and A D E F be completed. I have shown (in the 8th article of chapter XVI) that the body will be carried from E to A by the concourse of two uniform motions, the one in E F and its parallels, the other in E D and its parallels. But the motion in E F and its parallels, whereof D A is one, contributes nothing to the body in A to make it endeavour or press towards B; and therefore the whole endeavour, which the body hath in the inclined line E A to pass or press the strait line A D, it hath it all from the perpendicular motion or endeavour in F A. Wherefore the body E, after it is in A, will have only that perpendicular endeavour which proceeds from the motion in F A, that is, in A B; which was to be proved.

7. If a hard body falling upon or pressing another body penetrate the same, its endeavour after its first penetration will be neither in the inclined line produced, nor in the perpendicular, but sometimes betwixt both, sometimes without them.

Let E A G (in the same fig. 1) be the inclined line produced; and first, let the passage through the medium, in which E A is, be easier than the passage through the medium in which A G is. As soon therefore as the body is within the medium in which is A G, it will find greater resistance to its motion in D A and its parallels, than it did whilst it was above A D; and therefore below A D it will proceed with slower motion in the parallels of D A, than above it. Wherefore the motion which is compounded of the two motions in E F and E D will be slower below A D than above it; and therefore also, the body will not proceed from A in E A produced, but below it. Seeing, therefore, the endeavour in A B is generated by the endeavour in F A; if to the endeavour in F A there be added the endeavour in D A, which is not all taken away by the immersion of the point A into the lower medium, the body will not proceed from A in the perpendicular A B, but beyond it; namely, in some strait line between A B and A G, as in the line A H.

Secondly, let the passage through the medium E A be less easy than that through A G. The motion, therefore, which is made by the concourse of the motions in E F and F B, is slower above A D than below it; and consequently, the endeavour will not proceed from A in E A produced, but beyond it, as in A I. Wherefore, if a hard body falling, &c.; which was to be proved.

This divergency of the strait line A H from the strait line A G is that which, the writers of optics commonly called refraction, which, when the passage is easier in the first than in the second medium, is made by diverging from the line of inclination towards the perpendicular; and contrarily, when the passage is not so easy in the first medium, by departing further from the perpendicular.

8. By the 6th theorem it is manifest, that the force of the movent may be so placed, as that the body moved by it may proceed in a way almost directly contrary to that of the movent, as we see in the motion of ships.

For let A B (in fig. 2) represent a ship, whose length from the prow to the poop is A B, and let the wind lie upon it in the strait parallel lines C B, D E and F G; and let D E and F G be cut in E andand G by a strait line drawn from B perpendicular to A B; also let B E and E G be equal, and the angle A B C any angle how small soever. Then between B C and B A let the strait line B I be drawn; and let the sail be conceived to be spread in the same line B I, and the wind to fall upon it in the points L, M and B; from which points, perpendicular to B I, let B K, M Q and L P be drawn. Lastly, let E N and G O be drawn perpendicular to B G, and cutting B K in H and K; and let H N and K O be made equal to one another, and severally equal to B A. I say, the ship B A, by the wind falling upon it in C B, D E, F G, and other lines parallel to them, will be carried forwards almost opposite to the wind, that is to say, in a way almost contrary to the way of the movent.

For the wind that blows in the line C B will (as hath been shown in art. 6) give to the point B an endeavour to proceed in a strait line perpendicular to the strait line B I, that is, in the strait line B K; and to the points M and L an endeavour to proceed in the strait lines M Q and L P, which are parallel to B K. Let now the measure of the time be B G, which is divided in the middle in E; and let the point B be carried to H in the time B E. In the same time, therefore, by the wind blowing in D M and F L, and as many other lines as may be drawn parallel to them, the whole ship will be applied to the strait line H N. Also at the end of the second time E G, it will be applied to the strait line K O. Wherefore the ship will always go forward; and the angle it makes with the wind will be equal to the angle A B C, how small soever that angle be; and the way it makes will in every time be equal to the strait line E H. I say, thus it would be, if the ship might be moved with as great celerity sideways from B A towards K O, as it may be moved forwards in the line B A. But this is impossible, by reason of the resistance made by the great quantity of water which presseth the side, much exceeding the resistance made by the much smaller quantity which presseth the prow of the ship; so that the way the ship makes sideways is scarce sensible; and, therefore, the point B will proceed almost in the very line B A, making with the wind the angle A B C, how acute soever; that is to say, it will proceed almost in the strait line B C, that is, in a way almost contrary to the way of the movent; which was to be demonstrated.

But the sail in B I must be so stretched as that there be left in it no bosom at all; for otherwise the strait lines L P, M Q and B K will not be perpendicular to the plane of the sail, but falling below P, Q and K, will drive the ship backwards. But by making use of a small board for a sail, a little waggon with wheels for the ship, and of a smooth pavement for the sea, I have by experience found this to be so true, that I could scarce oppose the board to the wind in any obliquity, though never so small, but the waggon was carried forwards by it.

By the same 6th theorem it may be found, how much a stroke, which falls obliquely, is weaker than a stroke falling perpendicularly, they being like and equal in all other respects.

Let a stroke fall upon the wall A B obliquely, as for example, in the strait line C A (in fig. 3.) Let C E be drawn parallel to A B, and D A perpendicular to the same A B and equal to C A; and let both the velocity and time of the motion in C A be equal to the velocity and time of the motion in D A. I say, the stroke in C A will be weaker than that in D A, in the proportion of E A to D A. For producing D A howsoever to F, the endeavour of both the strokes will (by art. 6) proceed from A in the perpendicular A F. But the stroke in C A is made by the concourse of two motions in C E and E A, of which that in C E contributes nothing to the stroke in A, because C E and B A are parallels; and, therefore, the stroke in C A is made by the motion which is in E A only. But the velocity or force of the perpendicular stroke in E A, to the velocity or force of the stroke in D A, is as E A to D A. Wherefore the oblique stroke in C A is weaker than the perpendicular stroke in D A, in the proportion of E A to D A or C A; which was to be proved.