9. In a full medium, all endeavour proceeds as far as the medium itself reacheth; that is to say, if the medium be infinite, the endeavour will proceed infinitely.

For whatsoever endeavoureth is moved, and therefore whatsoever standeth in its way it maketh it yield, at least a little, namely, so far as the movent itself is moved forwards. But that which yieldeth is also moved, and consequently maketh that to yield which is in its way, and so on successively as long as the medium is full; that is to say, infinitely, if the full medium be infinite; which was to be proved.

Now although endeavour thus perpetually propagated do not always appear to the senses as motion, yet it appears as action, or as the efficient cause of some mutation. For if there be placed before our eyes some very little object, as for example, a small grain of sand, which at a certain distance is visible; it is manifest that it may be removed to such a distance as not to be any longer seen, though by its action it still work upon the organs of sight, as is manifest from that which was last proved, that all endeavour proceeds infinitely. Let it be conceived therefore to be removed from our eyes to any distance how great soever, and a sufficient number of other grains of sand of the same bigness added to it; it is evident that the aggregate of all those sands will be visible; and though none of them can be seen when it is single and severed from the rest, yet the whole heap or hill which they make will manifestly appear to the sight; which would be impossible, if some action did not proceed from each several part of the whole heap.

10. Between the degrees of hard and soft are those things which we call tough, tough being that which may be bent without being altered from what it was; and the bending of a line is either the adduction or diduction of the extreme parts, that is, a motion from straitness to crookedness, or contrarily, whilst the line remains still the same it was; for by drawing out the extreme points of a line to their greatest distance, the line is made strait, which otherwise is crooked. So also the bending of a superficies is the diduction or adduction of its extreme lines, that is, their dilatation and contraction.

11. Dilatation and contraction, as also all flexion, supposes necessarily that the internal parts of the body bowed do either come nearer to the external parts, or go further from them. For though flexion be considered only in the length of a body, yet when that body is bowed, the line which is made on one side will be convex, and the line on the other side will be concave; of which the concave, being the interior line, will, unless something be taken from it and added to the convex line, be the more crooked, that is, the greater of the two. But they are equal; and, therefore, in flexion there is an accession made from the interior to the exterior parts; and, on the contrary, in tension, from the exterior to the interior parts. And as for those things which do not easily suffer such transposition of their parts, they are called brittle; and the great force they require to make them yield, makes them also with sudden motion to leap asunder, and break in pieces.

12. Also motion is distinguished into pulsion and traction. And pulsion, as I have already defined it, is when that which is moved goes before that which moveth it. But contrarily, in traction the movent goes before that which is moved. Nevertheless, considering it with greater attention, it seemeth to be the same with pulsion. For of two parts of a hard body, when that which is foremost drives before it the medium in which the motion is made, at the same time that which is thrust forwards thrusteth the next, and this again the next, and so on successively. In which action, if we suppose that there is no place void, it must needs be, that by continual pulsion, namely, when that action has gone round, the movent will be behind that part, which at the first seemed not to be thrust forwards, but to be drawn; so that now the body, which was drawn, goes before the body which gives it motion; and its motion is no longer traction, but pulsion.

13. Such things as are removed from their places by forcible compression or extension, and, as soon as the force is taken away, do presently return and restore themselves to their former situation, have the beginning of their restitution within themselves, namely, a certain motion in their internal parts, which was there, when, before the taking away of the force, they were compressed, or extended. For that restitution is motion, and that which is at rest cannot be moved, but by a moved and a contiguous movent. Nor doth the cause of their restitution proceed from the taking away of the force by which they were compressed or extended; for the removing of impediments hath not the efficacy of a cause, as has been shown at the end of the 3rd article of chap. XV. The cause therefore of their restitution is some motion either of the parts of the ambient, or of the parts of the body compressed or extended. But the parts of the ambient have no endeavour which contributes to their compression or extension, nor to the setting of them at liberty, or restitution. It remains therefore that from the time of their compression or extension there be left some endeavour or motion, by which, the impediment being removed, every part resumes its former place; that is to say, the whole restores itself.

14. In the carriage of bodies, if that body, which carries another, hit upon any obstacle, or be by any means suddenly stopped, and that which is carried be not stopped, it will go on, till its motion be by some external impediment taken away.

For I have demonstrated (chap. VIII, art. 19) that motion, unless it be hindered by some external resistance, will be continued eternally with the same celerity; and in the 7th article of chap. IX, that the action of an external agent is of no effect without contact. When therefore that, which carrieth another thing, is stopped, that stop doth not presently take away the motion of that which is carried. It will therefore proceed, till its motion be by little and little extinguished by some external resistance: which was to be proved; though experience alone had been sufficient to prove this.

In like manner, if that body which carrieth another be put from rest into sudden motion, that which is carried will not be moved forwards together with it, but will be left behind. For the contiguous part of the body carried hath almost the same motion with the body which carries it; and the remote parts will receive different velocities according to their different distances from the body that carries them; namely, the more remote the parts are, the less will be their degrees of velocity. It is necessary, therefore, that the body, which is carried, be left accordingly more or less behind. And this also is manifest by experience, when at the starting forward of the horse the rider falleth backwards.

15. In percussion, therefore, when one hard body is in some small part of it stricken by another with great force, it is not necessary that the whole body should yield to the stroke with the same celerity with which the stricken part yields. For the rest of the parts receive their motion from the motion of the part stricken and yielding, which motion is less propagated every way towards the sides, than it is directly forwards. And hence it is, that sometimes very hard bodies, which being erected can hardly be made to stand, are more easily broken than thrown down by a violent stroke; when, nevertheless, if all their parts together were by any weak motion thrust forwards, they would easily be cast down.

16. Though the difference between trusion and percussion consist only in this, that in trusion the motion both of the movent and moved body begin both together in their very contact; and in percussion the striking body is first moved, and afterwards the body stricken; yet their effects are so different, that it seems scarce possible to compare their forces with one another. I say, any effect of percussion being propounded, as for example, the stroke of a beetle of any weight assigned, by which a pile of any given length is to be driven into earth of any tenacity given, it seems to me very hard, if not impossible, to define with what weight, or with what stroke, and in what time, the same pile may be driven to a depth assigned into the same earth. The cause of which difficulty is this, that the velocity of the percutient is to be compared with the magnitude of the ponderant. Now velocity, seeing it is computed by the length of space transmitted, is to be accounted but as one dimension; but weight is as a solid thing, being measured by the dimension of the whole body. And there is no comparison to be made of a solid body with a length, that is, with a line.

17. If the internal parts of a body be at rest, or retain the same situation with one another for any time how little soever, there cannot in those parts be generated any new motion or endeavour, whereof the efficient cause is not without the body of which they are parts. For if any small part, which is comprehended within the superficies of the whole body, be supposed to be now at rest, and by and by to be moved, that part must of necessity receive its motion from some moved and contiguous body. But by supposition, there is no such moved and contiguous part within the body. Wherefore, if there be any endeavour or motion or change of situation in the internal parts of that body, it must needs arise from some efficient cause that is without the body which contains them; which was to be proved.

18. In hard bodies, therefore, which are compressed or extended, if, that which compresseth or extendeth them being taken away, they restore themselves to their former place or situation, it must needs be that that endeavour or motion of their internal parts, by which they were able to recover their former places or situations, was not extinguished when the force by which they were compressed or extended was taken away. Therefore, when the lath of a cross-bow bent doth, as soon as it is at liberty, restore itself, though to him, that judges by sense, both it and all its parts seem to be at rest; yet he, that judging by reason doth not account the taking away of impediment for an efficient cause, nor conceives that without an efficient cause any thing can pass from rest to motion, will conclude that the parts were already in motion before they began to restore themselves.

19. Action and reaction proceed in the same line, but from opposite terms. For seeing reaction is nothing but endeavour in the patient to restore itself to that situation from which it was forced by the agent; the endeavour or motion both of the agent and patient or reagent will be propagated between the same terms; yet so, as that in action the term, from which, is in reaction the term to which. And seeing all action proceeds in this manner, not only between the opposite terms of the whole line in which it is propagated, but also in all the parts of that line, the terms from which and to which, both of the action and reaction, will be in the same line. Wherefore action and reaction proceed in the same line, &c.

20. To what has been said of motion, I will add what I have to say concerning habit. Habit, therefore, is a generation of motion, not of motion simply, but an easy conducting of the moved body in a certain and designed way. And seeing it is attained by the weakening of such endeavours as divert its motion, therefore such endeavours are to be weakened by little and little. But this cannot be done but by the long continuance of action, or by actions often repeated; and therefore custom begets that facility, which is commonly and rightly called habit; and it may be defined thus: HABIT is motion made more easy and ready by custom; that is to say, by perpetual endeavour, or by iterated endeavours in a way differing from that in which the motion proceeded from the beginning, and opposing such endeavours as resist. And to make this more perspicuous by example, we may observe, that when one that has no skill in music first puts his hand to an instrument, he cannot after the first stroke carry his hand to the place where he would make the second stroke, without taking it back by a new endeavour, and, as it were beginning again, pass from the first to the second. Nor will he be able to go on to the third place without another new endeavour; but he will be forced to draw back his hand again, and so successively, by renewing his endeavour at every stroke; till at the last, by doing this often, and by compounding many interrupted motions or endeavours into one equal endeavour, he be able to make his hand go readily on from stroke to stroke in that order and way which was at the first designed. Nor are habits to be observed in living creatures only, but also in bodies inanimate. For we find that when the lath of a cross-bow is strongly bent, and would if the impediment were removed return again with great force; if it remain a long time bent, it will get such a habit, that when it is loosed and left to its own freedom, it will not only not restore itself, but will require as much force for the bringing of it back to its first posture, as it did for the bending of it at the first.

Vol. 1. Lat. & Eng.
C. XXII.
Fig. 1-3

CHAP. XXIII.

OF THE CENTRE OF EQUIPONDERATION; OF
BODIES PRESSING DOWNWARDS IN STRAIT
PARALLEL LINES.

1. Definitions and suppositions.—2. Two planes of equiponderation are not parallel.—3. The centre of equiponderation is in every plane of equiponderation.—4. The moments of equal ponderants are to one another as their distances from the centre of the scale.—5, 6. The moments of unequal ponderants have their proportion to one another compounded of the proportions of their weights and distances from the centre of the scale.—7. If two ponderants have their weights and distances from the centre of the scale in reciprocal proportion, they are equally poised; and contrarily.—8. If the parts of any ponderant press the beams of the scale every where equally, all the parts cut off, reckoned from the centre of the scale, will have their moments in the same proportion with that of the parts of a triangle cut off from the vertex by strait lines parallel to the base.—9. The diameter of equiponderation of figures, which are deficient according to commensurable proportions of their altitudes and bases, divides the axis, so that the part taken next the vertex is to the other part of the complete figure to the deficient figure.—10. The diameter of equiponderation of the complement of the half of any of the said deficient figures, divides that line which is drawn through the vertex parallel to the base, so that the part next the vertex is to the other part as the complete figure to the complement.—11. The centre of equiponderation of the half of any of the deficient figures in the first row of the table of art. 3, chap. XVII, may be found out by the numbers of the second row.—12. The centre of equiponderation of the half of any of the figures of the second row of the same table, may be found out by the numbers of the fourth row.—13. The centre of equiponderation of the half of any of the figures in the same table being known, the centre of the excess of the same figure above a triangle of the same altitude and base is also known.—14. The centre of equiponderation of a solid sector is in the axis so divided, that the part next the vertex be to the whole axis, wanting half the axis of the portion of the sphere, as 3 to 4.

I. A scale is a strait line, whose middle point is immovable, all the rest of its points being at liberty; and that part of the scale, which reaches from the centre to either of the weights, is called the beam.

II. Equiponderation is when the endeavour of one body, which presses one of the beams, resists the endeavour of another body pressing the other beam, so that neither of them is moved; and the bodies, when neither of them is moved, are said to be equally poised.

III. Weight is the aggregate of all the endeavours, by which all the points of that body, which presses the beam, tend downwards in lines parallel to one another; and the body which presses is called the ponderant.

IV. Moment is the power which the ponderant has to move the beam, by reason of a determined situation.

V. The plane of equiponderation is that by which the ponderant is so divided, that the moments on both sides remain equal.

VI. The diameter of equiponderation is the common section of the two planes of equiponderation, and is in the strait line by which the weight is hanged.

VII. The centre of equiponderation is the common point of the two diameters of equiponderation.

I. When two bodies are equally poised, if weight be added to one of them and not to the other, their equiponderation ceases.

II. When two ponderants of equal magnitude, and of the same species or matter, press the beam on both sides at equal distances from the centre of the scale, their moments are equal. Also when two bodies endeavour at equal distances from the centre of the scale, if they be of equal magnitude and of the same species, their moments are equal.

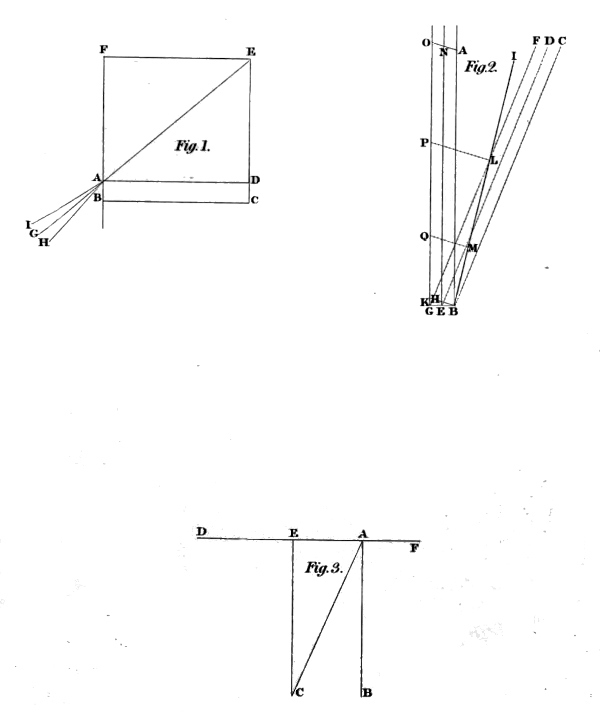
2. No two planes of equiponderation are parallel.

Let A B C D (in fig. 1) be any ponderant whatsoever; and in it let E F be a plane of equiponderation; parallel to which, let any other plane be drawn, as G H. I say, G H is not a plane of equiponderation. For seeing the parts A E F D and E B C F of the ponderant A B C D are equally poised; and the weight E G H F is added to the part A E F D, and nothing is added to the part E B C F, but the weight E G H F is taken from it; therefore, by the first supposition, the parts A G H D and G B C H will not be equally poised; and consequently G H is not a plane of equiponderation. Wherefore, no two planes of equiponderation are parallel; which was to be proved.

3. The centre of equiponderation is in every plane of equiponderation.

For if another plane of equiponderation be taken, it will not, by the last article, be parallel to the former plane; and therefore both those planes will cut one another. Now that section (by the 6th definition) is the diameter of equiponderation. Again, if another diameter of equiponderation be taken, it will cut that former diameter; and in that section (by the 7th definition) is the centre of equiponderation. Wherefore the centre of equiponderation is in that diameter which lies in the said plane of equiponderation.

4. The moment of any ponderant applied to one point of the beam, to the moment of the same or an equal ponderant applied to any other point of the beam, is as the distance of the former point from the centre of the scale, to the distance of the latter point from the same centre. Or thus, those moments are to one another, as the arches of circles which are made upon the centre of the scale through those points, in the same time. Or lastly thus, they are as the parallel bases of two triangles, which have a common angle at the centre of the scale.

Let A (in fig. 2) be the centre of the scale; and let the equal ponderants D and E press the beam A B in the points B and C; also let the strait lines B D and C E be diameters of equiponderation; and the points D and E in the ponderants D and E be their centres of equiponderation. Let A G F be drawn howsoever, cutting D B produced in F, and E C in G; and lastly, upon the common centre A, let the two arches B H and C I be described, cutting A G F in H and I. I say, the moment of the ponderant D to the moment of the ponderant E is as A B to A C, or as B H to C I, or as B F to C G. For the effect of the ponderant D, in the point B, is circular motion in the arch B H; and the effect of the ponderant E, in the point C, circular motion in the arch C I; and by reason of the equality of the ponderants D and E, these motions are to one another as the quicknesses or velocities with which the points B and C describe the arches B H and C I, that is, as the arches themselves B H and C I, or as the strait parallels B F and C G, or as the parts of the beam A B and A C; for A B. A C:: B F. C G:: B H. C I. are proportionals; and therefore the effects, that is, by the 4th definition, the moments of the equal ponderants applied to several points of the beam, are to one another as A B and A C; or as the distances of those points from the centre of the scale; or as the parallel bases of the triangles which have a common angle at A; or as the concentric arches B H and C I; which was to be demonstrated.

5. Unequal ponderants, when they are applied to several points of the beam, and hang at liberty, that is, so as the line by which they hang be the diameter of equiponderation, whatsoever be the figure of the ponderant, have their moments to one another in proportion compounded of the proportions of their distances from the centre of the scale, and of their weights.

Let A (in fig. 3) be the centre of the scale, and A B the beam; to which let the two ponderants C and D be applied at the points B and E. I say, the proportion of the moment of the ponderant C to the moment of the ponderant D, is compounded of the proportions of A B to A E, and of the weight C to the weight D; or, if C and D be of the same species, of the magnitude C to the magnitude D.

Let either of them, as C, be supposed to be bigger than the other, D. If, therefore, by the addition of F, F and D together be as one body equal to C, the moment of C to the moment of F + D will be (by the last article) as B G is to E H. Now as F + D is to D, so let E H be to another E I; and the moment of F + D, that is of C, to the moment of D, will be as B G to E I. But the proportion of B G to E I is compounded of the proportions of B G to E H, that is, of A B to A E, and of E H to E I, that is, of the weight C to the weight D. Wherefore unequal ponderants, when they are applied, &c. Which was to be proved.

6. The same figure remaining, if I K be drawn parallel to the beam A B, and cutting A G in K; and K L be drawn parallel to B G, cutting A B in L, the distances A B and A L from the centre will be proportional to the moments of C and D. For the moment of C is B G, and the moment of D is E I, to which K L is equal. But as the distance A B from the centre is to the distance A L from the centre, so is B G, the moment of the ponderant C, to L K, or E I the moment of the ponderant D.

7. If two ponderants have their weights and distances from the centre in reciprocal proportion, and the centre of the scale be between the points to which the ponderants are applied, they will be equally poised. And contrarily, if they be equally poised, their weights and distances from the centre of the scale will be in reciprocal proportion.

Let the centre of the scale (in the same third figure) be A, the beam A B; and let any ponderant C, having B G for its moment, be applied to the point B; also let any other ponderant D, whose moment is E I, be applied to the point E. Through the point I let I K be drawn parallel to the beam A B, cutting A G in K; also let K L be drawn parallel to B G, K L will then be the moment of the ponderant D; and by the last article, it will be as B G, the moment of the ponderant C in the point B, to L K the moment of the ponderant D in the point E, so A B to A L. On the other side of the centre of the scale, let A N be taken equal to A L; and to the point N let there be applied the ponderant O, having to the ponderant C the proportion of A B to A N. I say, the ponderants in B and N will be equally poised. For the proportion of the moment of the ponderant O, in the point N, to the moment of the ponderant C in the point B, is by the 5th article, compounded of the proportions of the weight O to the weight C, and of the distance from the centre of the scale A N or A L to the distance from the centre of the scale A B. But seeing we have supposed, that the distance A B to the distance A N is in reciprocal proportion of the weight O to the weight C, the proportion of the moment of the ponderant O, in the point N, to the moment of the ponderant C, in the point B, will be compounded of the proportions of A B to A N, and of A N to A B. Wherefore, setting in order A B, A N, A B, the moment of O to the moment of C will be as the first to the last, that is, as A B to A B. Their moments therefore are equal; and consequently the plane which passes through A will (by the fifth definition) be a plane of equiponderation. Wherefore they will be equally poised; as was to be proved.

Now the converse of this is manifest. For if there be equiponderation and the proportion of the weights and distances be not reciprocal, then both the weights will always have the same moments, although one of them have more weight added to it or its distance changed.

Coroll. When ponderants are of the same species, and their moments be equal; their magnitudes and distances from the centre of the scale will be reciprocally proportional. For in homogeneous bodies, it is as weight to weight, so magnitude to magnitude.

8. If to the whole length of the beam there be applied a parallelogram, or a parallelopipedum, or a prisma, or a cylinder, or the superficies of a cylinder, or of a sphere, or of any portion of a sphere or prisma; the parts of any of them cut off with planes parallel to the base will have their moments in the same proportion with the parts of a triangle, which has its vertex in the centre of the scale, and for one of its sides the beam itself, which parts are cut off by planes parallel to the base.

First, let the rectangled parallelogram A B C D (in figure 4) be applied to the whole length of the beam A B; and producing C B howsoever to E, let the triangle A B E be described. Let now any part of the parallelogram, as A F, be cut off by the plane F G, parallel to the base C B; and let F G be produced to A E in the point H. I say, the moment of the whole A B C D to the moment of its part A F, is as the triangle A B E to the triangle A G H, that is, in proportion duplicate to that of the distances from the centre of the scale.

For, the parallelogram A B C D being divided into equal parts, infinite in number, by strait lines drawn parallel to the base; and supposing the moment of the strait line C B to be B E, the moment of the strait line F G will (by the 7th article) be G H; and the moments of all the strait lines of that parallelogram will be so many strait lines in the triangle A B E drawn parallel to the base B E; all which parallels together taken are the moment of the whole parallelogram A B C D; and the same parallels do also constitute the superficies of the triangle A B E. Wherefore the moment of the parallelogram A B C D is the triangle A B E; and for the same reason, the moment of the parallelogram A F is the triangle A G H; and therefore the moment of the whole parallelogram to the moment of a parallelogram which is part of the same, is as the triangle A B E to the triangle A G H, or in proportion duplicate to that of the beams to which they are applied. And what is here demonstrated in the case of a parallelogram may be understood to serve for that of a cylinder, and of a prisma, and their superficies; as also for the superficies of a sphere, of an hemisphere, or any portion of a sphere. For the parts of the superficies of a sphere have the same proportion with that of the parts of the axis cut off by the same parallels, by which the parts of the superficies are cut off, as Archimedes has demonstrated; and therefore when the parts of any of these figures are equal and at equal distances from the centre of the scale, their moments also are equal, in the same manner as they are in parallelograms.

Secondly, let the parallelogram A K I B not be rectangled; the strait line I B will nevertheless press the point B perpendicularly in the strait line B E; and the strait line L G will press the point G perpendicularly in the strait line G H; and all the rest of the strait lines which are parallel to I B will do the like. Whatsoever therefore the moment be which is assigned to the strait line I B, as here, for example, it is supposed to be B E, if A E be drawn, the moment of the whole parallelogram A I will be the triangle A B E; and the moment of the part A L will be the triangle A G H. Wherefore the moment of any ponderant, which has its sides equally applied to the beam, whether they be applied perpendicularly or obliquely, will be always to the moment of a part of the same in such proportion as the whole triangle has to a part of the same cut off by a plane which is parallel to the base.

9. The centre of equiponderation of any figure, which is deficient according to commensurable proportions of the altitude and base diminished, and whose complete figure is either a parallelogram or a cylinder, or a parallelopipedum, divides the axis, so, that the part next the vertex, to the other part, is as the complete figure to the deficient figure.

For let C I A P E (in fig. 5) be a deficient figure, whose axis is A B, and whose complete figure is C D F E; and let the axis A B be so divided in Z, that A Z be to Z B as C D F E is to C I A P E. I say, the centre of equiponderation of the figure C I A P E will be in the point Z.

First, that the centre of equiponderation of the figure C I A P E is somewhere in the axis A B is manifest of itself; and therefore A B is a diameter of equiponderation. Let A E be drawn, and let B E be put for the moment of the strait line C E; the triangle A B E will therefore (by the third article) be the moment of the complete figure C D F E. Let the axis A B be equally divided in L, and let G L H be drawn parallel and equal to the strait line C E, cutting the crooked line C I A P E in I and P, and the strait lines A C and A E in K and M. Moreover, let Z O be drawn parallel to the same C E; and let it be, as L G to L I, so L M to another, L N; and let the same be done in all the rest of the strait lines possible, parallel to the base; and through all the points N, let the line A N E be drawn; the three-sided figure A N E B will therefore be the moment of the figure C I A P E. Now the triangle A B E is (by the 9th article of chapter XVII) to the three-sided figure A N E B, as A B C D + A I C B is to A I C B twice taken, that is, as C D F E + C I A P E is to C I A P E twice taken. But as C I A P E is to C D F E, that is, as the weight of the deficient figure is to the weight of the complete figure, so is C I A P E twice taken to C D F E twice taken. Wherefore, setting in order C D F E + C I A P E. 2 C I A P E. 2 C D F E; the proportion of C D F E + C I A P E to C D F E twice taken will be compounded of the proportion of C D F E + C I A P E to C I A P E twice taken, that is, of the proportion of the triangle A B E to the three-sided figure A N E B, that is, of the moment of the complete figure to the moment of the deficient figure, and of the proportion of C I A P E twice taken to C D F E twice taken, that is, to the proportion reciprocally taken of the weight of the deficient figure to the weight of the complete figure.

Again, seeing by supposition A Z. Z B:: C D F E. C I A P E are proportionals; A B. A Z:: C D F E + C I A P E. C D F E will also, by compounding, be proportionals. And seeing A L is the half of A B, A L. A Z:: C D F E + C I A P E. 2 C D F E will also be proportionals. But the proportion of C D F E + C I A P E to 2 C D F E is compounded, as was but now shown, of the proportions of moment to moment, &c., and therefore the proportion of A L to A Z is compounded of the proportion of the moment of the complete figure C D F E to the moment of the deficient figure C I A P E, and of the proportion of the weight of the deficient figure C I A P E to the weight of the complete figure C D F E; but the proportion of A L to A Z is compounded of the proportions of A L to B Z and of B Z to A Z. Now the proportion of B Z to A Z is the proportion of the weights reciprocally taken, that is to say, of the weight C I A P E to the weight C D F E. Therefore the remaining proportion of A L to B Z, that is, of L B to B Z, is the proportion of the moment of the weight C D F E to the moment of the weight C I A P E. But the proportion of A L to B Z is compounded of the proportions of A L to A Z and of A Z to Z B; of which proportions that of A Z to Z B is the proportion of the weight C D F E to the weight C I A P E. Wherefore (by art. 5 of this chapter) the remaining proportion of A L to A Z is the proportion of the distances of the points Z and L from the centre of the scale, which is A. And, therefore, (by art. 6) the weight C I A P E shall hang from O in the strait line O Z. So that O Z is one diameter of equiponderation of the weight C I A P E. But the strait line A B is the other diameter of equiponderation of the same weight C I A P E. Wherefore (by the 7th definition) the point Z is the centre of the same equiponderation; which point, by construction, divides the axis so, that the part A Z, which is the part next the vertex, is to the other part Z B, as the complete figure C D F E is to the deficient figure C I A P E; which is that which was to be demonstrated.

Coroll. I. The centre of equiponderation of any of those plane three-sided figures, which are compared with their complete figures in the table of art. 3, chap. XVII, is to be found in the same table, by taking the denominator of the fraction for the part of the axis cut off next the vertex, and the numerator for the other part next the base. For example, if it be required to find the centre of equiponderation of the second three-sided figure of four means, there is in the concourse of the second column with the row of three-sided figures of four means this fraction ⁵⁄₇, which signifies that that figure is to its parallelogram or complete figure as ⁵⁄₇ to unity, that is, as ⁵⁄₇ to ⁷⁄₇, or as 5 to 7; and, therefore the centre of equiponderation of that figure divides the axis, so that the part next the vertex is to the other part as 7 to 5.

Coroll. II. The centre of equiponderation of any of the solids of those figures, which are contained in the table of art. 7 of the same chap. XVII, is exhibited in the same table. For example, if the centre of equiponderation of a cone be sought for, the cone will be found to be ¹⁄₃ of its cylinder; and, therefore, the centre of its equiponderation will so divide the axis, that the part next the vertex to the other part will be as 3 to 1. Also the solid of a three-sided figure of one mean, that is, a parabolical solid, seeing it is ²⁄₄, that is ½ of its cylinder, will have its centre of equiponderation in that point, which divides the axis, so that the part towards the vertex be double to the part towards the base.

10. The diameter of equiponderation of the complement of the half of any of those figures which are contained in the table of art. 3, chap. XVII, divides that line which is drawn through the vertex parallel and equal to the base, so that the part next the vertex will be to the other part, as the complete figure to the complement.

For let A I C B (in the same fig. 5) be the half of a parabola, or of any other of those three-sided figures which are in the table of art. 3, chap. XVII, whose axis is A B, and base B C, having A D drawn from the vertex, equal and parallel to the base B C, and whose complete figure is the parallelogram A B C D. Let I Q be drawn at any distance from the side C D, but parallel to it; and let A D be the altitude of the complement A I C D, and Q I a line ordinately applied in it. Wherefore the altitude A L in the deficient figure A I C B is equal to Q I the line ordinately applied in its complement; and contrarily, L I the line ordinately applied in the figure A I C B is equal to the altitude A Q in its complement; and so in all the rest of the ordinate lines and altitudes the mutation is such, that that line, which is ordinately applied in the figure, is the altitude of its complement. And, therefore, the proportion of the altitudes decreasing to that of the ordinate lines decreasing, being multiplicate according to any number in the deficient figure, is submultiplicate according to the same number in its complement. For example, if A I C B be a parabola, seeing the proportion of A B to A L is duplicate to that of B C to L I, the proportion of AD to A Q in the complement A I C D, which is the same with that of B C to L I, will be subduplicate to that of C D to Q I, which is the same with that of A B to A L; and consequently, in a parabola, the complement will be to the parallelogram as 1 to 3; in a three-sided figure of two means, as 1 to 4; in a three-sided figure of three means, as 1 to 5, &c. But all the ordinate lines together in A I C D are its moment; and all the ordinate lines in A I C B are its moment. Wherefore the moments of the complements of the halves of deficient figures in the table of art. 3 of chap. XVII, being compared, are as the deficient figures themselves; and, therefore, the diameter of equiponderation will divide the strait line A D in such proportion, that the part next the vertex be to the other part, as the complete figure A B C D is to the complement A I C D.

Coroll. The diameter of equiponderation of these halves may be found by the table of art. 3 of chap. XVII, in this manner. Let there be propounded any deficient figure, namely, the second three-sided figure of two means. This figure is to the complete figure as ³⁄₅ to 1, that is 3 to 5. Wherefore the complement to the same complete figure is as 2 to 5; and, therefore, the diameter of equiponderation of this complement will cut the strait line drawn from the vertex parallel to the base, so that the part next the vertex will be to the other part as 5 to 2. And, in like manner, any other of the said three-sided figures being propounded, if the numerator of its fraction found out in the table be taken from the denominator, the strait line drawn from the vertex is to be divided, so that the part next the vertex be to the other part, as the denominator is to the remainder which that subtraction leaves.