11. The centre of equiponderation of the half of any of those crooked-lined figures, which are in the first row of the table of art. 3 of chap. XVII, is in that strait line which, being parallel to the axis, divides the base according to the numbers of the fraction next below it in the second row, so that the numerator be answerable to that part which is towards the axis.
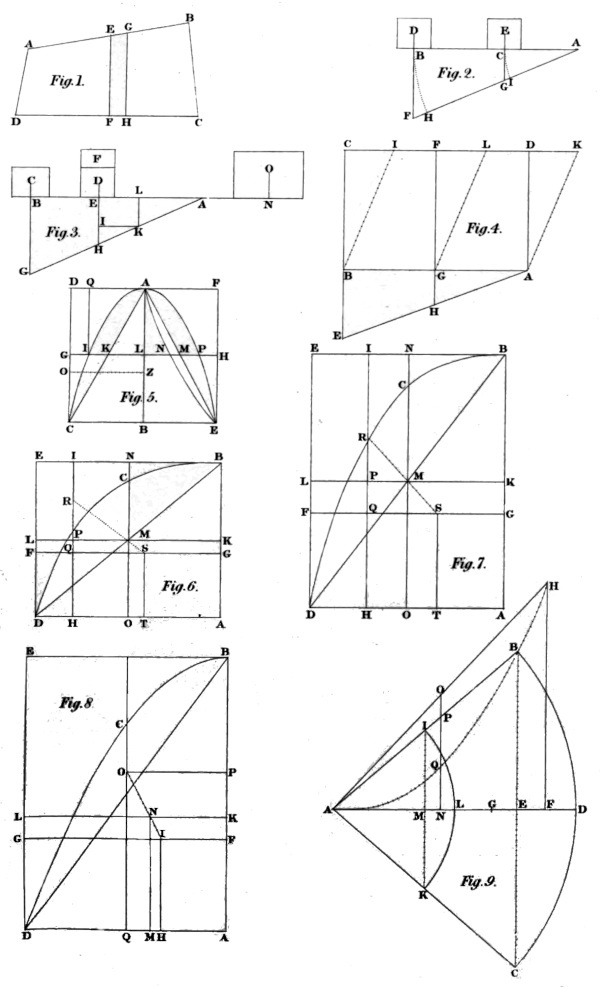
For example, let the first figure of three means be taken, whose half is A B C D (in fig. 6), and let the rectangle A B E D be completed. The complement therefore will be B C D E. And seeing A B E D is to the figure A B C D (by the table) as 5 to 4, the same A B E D will be to the complement B C D E as 5 to 1. Wherefore, if F G be drawn parallel to the base D A, cutting the axis so that A G be to G B as 4 to 5, the centre of equiponderation of the figure A B C D will, by the precedent article, be somewhere in the same F G. Again, seeing, by the same article, the complete figure A B E D, is to the complement B C D E as 5 to 1, therefore if B E and A D be divided in I and H as 5 to 1 the centre of equiponderation of the complement B C D E will be somewhere in the strait line which connects H and I. Let now the strait line L K be drawn through M the centre of the complete figure, parallel to the base; and the strait line N O through the same centre M, perpendicular to it; and let the strait lines L K and F G cut the strait line H I in P and Q. Let P R be taken quadruple to P Q; and let R M be drawn and produced to F G in S. R M therefore will be to M S as 4 to 1, that is, as the figure A B C D to its complement B C D E. Wherefore, seeing M is the centre of the complete figure A B E D, and the distances of R and S from the centre M be in proportion reciprocal to that of the weight of the complement B C D E to the weight of the figure A B C D, R and S will either be the centres of equiponderation of their own figures, or those centres will be in some other points of the diameters of equiponderation H I and F G. But this last is impossible. For no other strait line can be drawn through the point M terminating in the strait lines H I and F G, and retaining the proportion of M R to M S, that is, of the figure A B C D to its complement B C D E. The centre, therefore, of equiponderation of the figure A B C D is in the point S. Now, seeing P M hath the same proportion to Q S which R P hath to R Q, Q S will be 5 of those parts of which P M is four, that is, of which I N is four. But I N or P M is 2 of those parts of which E B or F G is 6; and, therefore, if it be as 4 to 5, so 2 to a fourth, that fourth will be 2½. Wherefore Q S is 2½ of those parts of which F G is 6. But F Q is 1; and, therefore, F S is 3½. Wherefore the remaining part G S is 2½. So that F G is so divided in S, that the part towards the axis is in proportion to the other part, as 2½ to 3½, that is as 5 to 7; which answereth to the fraction 5⁄7 in the second row, next under the fraction 4⁄5 in the first row. Wherefore drawing S T parallel to the axis, the base will be divided in like manner.
By this method it is manifest, that the base of a semiparabola will be divided into 3 and 5; and the base of the first three-sided figure of two means, into 4 and 6; and of the first three-sided figure of four means, into 6 and 8. The fractions, therefore, of the second row denote the proportions, into which the bases of the figures of the first row are divided by the diameters of equiponderation. But the first row begins one place higher than the second row.
12. The centre of equiponderation of the half of any of the figures in the second row of the same table of art. 3, chap. XVII, is in a strait line parallel to the axis, and dividing the base according to the numbers of the fraction in the fourth row, two places lower, so as that the numerator be answerable to that part which is next the axis.
Let the half of the second three-sided figure of two means be taken; and let it be A B C D (in fig. 7); whose complement is B C D E, and the rectangle completed A B E D. Let this rectangle be divided by the two strait lines L K and N O, cutting one another in the centre M at right angles; and because A B E D is to A B C D as 5 to 3, let A B be divided in G, so that A G to B G be as 3 to 5; and let F G be drawn parallel to the base. Also because A B E D is (by art. 9) to B C D E as 5 to 2, let B E be divided in the point I, so that B I be to I E as 5 to 2; and let I H be drawn parallel to the axis, cutting L K and F G in P and Q. Let now P R be so taken, that it be to P Q as 3 to 2, and let R M be drawn and produced to F G in S. Seeing, therefore, R P is to P Q, that is, R M to M S, as A B C D is to its complement B C D E, and the centres of equiponderation of A B C D and B C D E are in the strait lines F G and H I, and the centre of equiponderation of them both together in the point M; R will be the centre of the complement B C D E, and S the centre of the figure A B C D. And seeing P M, that is I N, is to Q S, as R P is to R Q; and I N or P M is 3 of those parts, of which B E, that is F G, is 14; therefore Q S is 5 of the same parts; and E I, that is F G, 4; and F S, 9; and G S, 5. Wherefore the strait line S T being drawn parallel to the axis, will divide the base A D into 5 and 9. But the fraction 5⁄9 is found in the fourth row of the table, two places below the fraction ⅗ in the second row.
By the same method, if in the same second row there be taken the second three-sided figure of three means, the centre of equiponderation of the half of it will be found to be in a strait line parallel to the axis, dividing the base according to the numbers of the fraction 6⁄10, two places below in the fourth row. And the same way serves for all the rest of the figures in the second row. In like manner, the centre of equiponderation of the third three-sided figure of three means will be found to be in a strait line parallel to the axis, dividing the base, so that the part next the axis be to the other part as 7 to 13, &c.
Coroll. The centres of equiponderation of the halves of the said figures are known, seeing they are in the intersection of the strait lines S T and F G, which are both known.
13. The centre of equiponderation of the half of any of the figures, which (in the table of art. 3, chap. XVII) are compared with their parallelograms, being known; the centre of equiponderation of the excess of the same figure above its triangle is also known.
For example, let the semiparabola A B C D (in fig. 8) be taken, whose axis is A B; whose complete figure is A B E D; and whose excess above its triangle is B C D B. Its centre of equiponderation may be found out in this manner. Let F G be drawn parallel to the base, so that A F be a third part of the axis; and let H I be drawn parallel to the axis, so that A H be a third part of the base. This being done, the centre of equiponderation of the triangle A B D will be I. Again, let K L be drawn parallel to the base, so that A K be to A B as 2 to 5; and M N parallel to the axis, so that A M be to A D as 3 to 8; and let M N terminate in the strait line K L. The centre, therefore, of equiponderation of the parabola A B C D is N; and therefore we have the centres of equiponderation of the semiparabola A B C D, and of its part the triangle A B D. That we may now find the centre of equiponderation of the remaining part B C D B, let I N be drawn and produced to O, so that N O be triple to I N; and O will be the centre sought for. For seeing the weight of A B D to the weight of B C D B is in proportion reciprocal to that of the strait line N O to the strait line I N; and N is the centre of the whole, and I the centre of the triangle A B D; O will be the centre of the remaining part, namely, of the figure B D C B; which was to be found.
Coroll. The centre of equiponderation of the figure B D C B is in the concourse of two strait lines, whereof one is parallel to the base, and divides the axis, so that the part next the base be ⅗ or 9⁄15 of the whole axis; the other is parallel to the axis, and so divides the base, that the part towards the axis be ½, or 12⁄24 of the whole base. For drawing O P parallel to the base, it will be as I N to N O, so F K to K P, that is, so 1 to 3, or 5 to 15. But A F is 5⁄15, or ⅓ of the whole A B; and A K is 6⁄15, or ⅖; and F K 1⁄15; and KP 3⁄15; and therefore A P is 9⁄15 of the axis A B. Also A H is ⅓, or 8⁄24; and A M ⅜, or 9⁄24 of the whole base; and therefore O Q being drawn parallel to the axis, M Q, which is triple to H M, will be 3⁄24. Wherefore A Q is 12⁄24, or ½ of the base A D.
The excesses of the rest of the three-sided figures in the first row of the table of art. 3, chap. XVII, have their centres of equiponderation in two strait lines, which divide the axis and base according to those fractions, which add 4 to the numerators of the fractions of a parabola 9⁄15 and 12⁄24; and 6 to the denominators, in this manner:—
| In a parabola, | the axis 9⁄15, the base 12⁄24. |
| In the first three-sided figure, | the axis 13⁄21, the base 16⁄30. |
| In the second three-sided figure, | the axis 17⁄27, the base 20⁄36, &c. |
And by the same method, any man, if it be worth the pains, may find out the centres of equiponderation of the excesses above their triangles of the rest of the figures in the second and third row, &c.
14. The centre of equiponderation of the sector of a sphere, that is, of a figure compounded of a right cone, whose vertex is the centre of the sphere, and the portion of the sphere whose base is the same with that of the cone, divides the strait line which is made of the axis of the cone and half the axis of the portion together taken, so that the part next the vertex be triple to the other part, or to the whole strait line as 3 to 4.
For let A B C (in fig. 9) be the sector of a sphere, whose vertex is the centre of the sphere A; whose axis is A D; and the circle upon B C is the common base of the portion of the sphere and of the cone whose vertex is A; the axis of which portion is E D, and the half thereof F D; and the axis of the cone, A E. Lastly, let A G be 3⁄4 of the strait line A F. I say, G is the centre of equiponderation of the sector A B C.
Let the strait line F H be drawn of any length, making right angles with A F at F; and drawing the strait line A H, let the triangle A F H be made. Then upon the same centre A let any arch I K be drawn, cutting A D in L; and its chord, cutting A D in M; and dividing M L equally in N, let N O be drawn parallel to the strait line F H, and meeting with the strait line A H in O.
Seeing now B D C is the spherical superficies of the portion cut off with a plane passing through B C, and cutting the axis at right angles; and seeing F H divides E D, the axis of the portion, into two equal parts in F; the centre of equiponderation of the superficies B D C will be in F (by art. 8); and for the same reason the centre of equiponderation of the superficies I L K, K being in the strait line A C, will be in N. And in like manner, if there were drawn, between the centre of the sphere A and the outermost spherical superficies of the sector, arches infinite in number, the centres of equiponderation of the spherical superficies, in which those arches are, would be found to be in that part of the axis, which is intercepted between the superficies itself and a plane passing along by the chord of the arch, and cutting the axis in the middle at right angles.
Let it now be supposed that the moment of the outermost spherical superficies B D C is F H. Seeing therefore the superficies B D C is to the superficies I L K in proportion duplicate to that of the arch B D C to the arch I L K, that is, of B E to I M, that is, of F H to N O; let it be as F H to N O, so N O to another N P; and again, as N O to N P, so N P to another N Q; and let this be done in all the strait lines parallel to the base F H thatthat can possibly be drawn between the base and the vertex of the triangle A F H. If then through all the points Q there be drawn the crooked line A Q H, the figure A F H Q A will be the complement of the first three-sided figure of two means; and the same will also be the moment of all the spherical superficies, of which the solid sector A B C D is compounded; and by consequent, the moment of the sector itself. Let now F H be understood to be the semidiameter of the base of a right cone, whose side is A H, and axis A F Wherefore, seeing the bases of the cones, which pass through F and N and the rest of the points of the axis, are in proportion duplicate to that of the strait lines F H and N O, &c., the moment of all the bases together, that is, of the whole cone, will be the figure itself A F H Q A; and therefore the centre of equiponderation of the cone A F H is the same with that of the solid sector. Wherefore, seeing A G is ¾ of the axis A F, the centre of equiponderation of the cone A F H is in G; and therefore the centre of the solid sector is in G also, and divides the part A F of the axis so that A G is triple to G F; that is, A G is to A F as 3 to 4; which was to be demonstrated.
Note, that when the sector is a hemisphere, the axis of the cone vanisheth into that point which is the centre of the sphere; and therefore it addeth nothing to half the axis of the portion. Wherefore, if in the axis of the hemisphere there be taken from the centre ¾ of half the axis, that is, ⅜ of the semidiameter of the sphere, there will be the centre of equiponderation of the hemisphere.
Vol. 1. Lat. & Eng.
C.XXIII.
Fig. 1-9
| Fig 1. | Fig 2. | Fig 3. | Fig 4. | Fig 5. | Fig 6. | Fig 7. | Fig 8. | Fig 9. |
CHAPTER XXIV.
OF REFRACTION AND REFLECTION.
1. Definitions.—2. In perpendicular motion there is no refraction.—3. Things thrown out of a thinner into a thicker medium are so refracted that the angle refracted is greater than the angle of inclination.—4. Endeavour, which from one point tendeth every way, will be so refracted, as that the sine of the angle refracted will be to the sine of the angle of inclination, as the density of the first medium is to the density of the second medium, reciprocally taken.—5. The sine of the refracted angle in one inclination is to the sine of the refracted angle in another inclination, as the sine of the angle of that inclination is to the sine of the angle of this inclination.—6. If two lines of incidence, having equal inclination, be the one in a thinner, the other in a thicker medium, the sine of the angle of inclination will be a mean proportional between the two sines of the refracted angles.—7. If the angle of inclination be semirect, and the line of inclination be in the thicker medium, and the proportion of their densities be the same with that of the diagonal to the side of a square, and the separating superficies be plane, the refracted line will be in the separating superficies.—8. If a body be carried in a strait line upon another body, and do not penetrate the same, but be reflected from it, the angle of reflection will be equal to the angle of incidence.—9. The same happens in the generation of motion in the line of incidence.
I. Refraction is the breaking of that strait line, in which a body is moved or its action would proceed in one and the same medium, into two strait lines, by reason of the different natures of the two mediums.
II. The former of these is called the line of incidence; the latter the refracted line. III. The point of refraction is the common point of the line of incidence, and of the refracted line.
IV. The refracting superficies, which also is the separating superficies of the two mediums, is that in which is the point of refraction.
V. The angle refracted is that, which the refracted line makes in the point of refraction with that line, which from the same point is drawn perpendicular to the separating superficies in a different medium.
VI. The angle of refraction is that which the refracted line makes with the line of incidence produced.
VII. The angle of inclination is that which the line of incidence makes with that line, which from the point of refraction is drawn perpendicular to the separating superficies.
VIII. The angle of incidence is the complement to a right angle of the angle of inclination.
And so, (in fig. 1) the refraction is made in A B F. The refracted line is B F. The line of incidence is A B. The point of incidence and of refraction is B. The refracting or separating superficies is D B E. The line of incidence produced directly is A B C. The perpendicular to the separating superficies is B H. The angle of refraction is C B F. The angle refracted is H B F. The angle of inclination is A B G or H B C. The angle of incidence is A B D.
IX. Moreover the thinner medium is understood to be that in which there is less resistance to motion, or to the generation of motion; and the thicker that wherein there is greater resistance.
X. And that medium in which there is equal resistance everywhere, is a homogeneous medium. All other mediums are heterogeneous.
If a body pass, or there be generation of motion from one medium to another of different density, in a line perpendicular to the separating superficies, there will be no refraction.
For seeing on every side of the perpendicular all things in the mediums are supposed to be like and equal, if the motion itself be supposed to be perpendicular, the inclinations also will be equal, or rather none at all; and therefore there can be no cause from which refraction may be inferred to be on one side of the perpendicular, which will not conclude the same refraction to be on the other side. Which being so, refraction on one side will destroy refraction on the other side; and consequently either the refracted line will be everywhere, which is absurd, or there will be no refracted line at all; which was to be demonstrated.
Coroll. It is manifest from hence, that the cause of refraction consisteth only in the obliquity of the line of incidence, whether the incident body penetrate both the mediums, or without penetrating, propagate motion by pressure only.
3. If a body, without any change of situation of its internal parts, as a stone, be moved obliquely out of the thinner medium, and proceed penetrating the thicker medium, and the thicker medium be such, as that its internal parts being moved restore themselves to their former situation; the angle refracted will be greater than the angle of inclination.
For let D B E (in the same first figure) be the separating superficies of two mediums; and let a body, as a stone thrown, be understood to be moved as is supposed in the strait line A B C; and let A B be in the thinner medium, as in the air; and B C in the thicker, as in the water. I say the stone, which being thrown, is moved in the line A B, will not proceed in the line B C, but in some other line, namely, that, with which the perpendicular B H makes the refracted angle H B F greater than the angle of inclination H B C.
For seeing the stone coming from A, and falling upon B, makes that which is at B proceed towards H, and that the like is done in all the strait lines which are parallel to B H; and seeing the parts moved restore themselves by contrary motion in the same line; there will be contrary motion generated in H B, and in all the strait lines which are parallel to it. Wherefore, the motion of the stone will be made by the concourse of the motions in A G, that is, in D B, and in G B, that is, in B H, and lastly, in H B, that is, by the concourse of three motions. But by the concourse of the motions in A G and B H, the stone will be carried to C; and therefore by adding the motion in H B, it will be carried higher in some other line, as in B F, and make the angle H B F greater than the angle H B C.
And from hence may be derived the cause, why bodies which are thrown in a very oblique line, if either they be any thing flat, or be thrown with great force, will, when they fall upon the water, be cast up again from the water into the air.
For let A B (in fig. 2) be the superficies of the water; into which, from the point C, let a stone be thrown in the strait line C A, making with the line B A produced a very little angle C A D; and producing B A indefinitely to D, let C D be drawn perpendicular to it, and A E parallel to C D. The stone therefore will be moved in C A by the concourse of two motions in C D and D A, whose velocities are as the lines themselves C D and D A. And from the motion in C D and all its parallels downwards, as soon as the stone falls upon A, there will be reaction upwards, because the water restores itself to its former situation. If now the stone be thrown with sufficient obliquity, that is, if the strait line C D be short enough, that is, if the endeavour of the stone downwards be less than the reaction of the water upwards, that is, less than the endeavour it hath from its own gravity (for that may be), the stone will by reason of the excess of the endeavour which the water hath to restore itself, above that which the stone hath downwards, be raised again above the superficies A B, and be carried higher, being reflected in a line which goes higher, as the line A G.
4. If from a point, whatsoever the medium be, endeavour be propagated every way into all the parts of that medium; and to the same endeavour there be obliquely opposed another medium of a different nature, that is, either thinner or thicker; that endeavour will be so refracted, that the sine of the angle refracted, to the sine of the angle of inclination, will be as the density of the first medium to the density of the second medium, reciprocally taken.
First, let a body be in the thinner medium in A (fig. 3), and let it be understood to have endeavour every way, and consequently, that its endeavour proceed in the lines A B and A b; to which let B b the superficies of the thicker medium be obliquely opposed in B and b, so that A B and A b be equal; and let the strait line B b be produced both ways. From the points B and b, let the perpendiculars B C and b c be drawn; and upon the centres B and b, and at the equal distances B A and b A, let the circles A C and A c be described, cutting B C and b c in C and c, and the same C B and c b produced in D and d, as also A B and A b produced in E and e. Then from the point A to the strait lines B C and b c let the perpendiculars A F and A f be drawn. A F therefore will be the sine of the angle of inclination of the strait line A B, and A f the sine of the angle of inclination of the strait line A h, which two inclinations are by construction made equal. I say, as the density of the medium in which are B C and b c is to the density of the medium in which are B D and b d, so is the sine of the angle refracted, to the sine of the angle of inclination.
Let the strait line F G be drawn parallel to the strait line A B, meeting with the strait line b B produced in G.
Seeing therefore A F and B G are also parallels, they will be equal; and consequently, the endeavour in A F is propagated in the same time, in which the endeavour in B G would be propagated if the medium were of the same density. But because B G is in a thicker medium, that is, in a medium which resists the endeavour more than the medium in which A F is, the endeavour will be propagated less in B G than in A F, according to the proportion which the density of the medium, in which A F is, hath to the density of the medium in which B G is. Let therefore the density of the medium, in which B G is, be to the density of the medium, in which A F is, as B G is to B H; and let the measure of the time be the radius of the circle. Let H I be drawn parallel to B D, meeting with the circumference in I; and from the point I let I K be drawn perpendicular to B D; which being done, B H and I K will be equal; and I K will be to A F, as the density of the medium in which is A F is to the density of the medium in which is I K. Seeing therefore in the time A B, which is the radius of the circle, the endeavour is propagated in A F in the thinner medium, it will be propagated in the same time, that is, in the time B I in the thicker medium from K to I. Therefore, B I is the refracted line of the line of incidence A B; and I K is the sine of the angle refracted; and A F the sine of the angle of inclination. Wherefore, seeing I K is to A F, as the density of the medium in which is A F to the density of the medium in which is I K; it will be as the density of the medium in which is A F or B C to the density of the medium in which is I K or B D, so the sine of the angle refracted to the sine of the angle of inclination. And by the same reason it may be shown, that as the density of the thinner medium is to the density of the thicker medium, so will K I the sine of the angle refracted be to A F the sine of the angle of inclination.
Secondly, let the body, which endeavoureth every way, be in the thicker medium at I. If, therefore, both the mediums were of the same density, the endeavour of the body in I B would tend directly to L; and the sine of the angle of inclination L M would be equal to I K or B H. But because the density of the medium, in which is I K, to the density of the medium, in which is L M, is as B H to B G, that is, to A F, the endeavour will be propagated further in the medium in which L M is, than in the medium in which I K is, in the proportion of density to density, that is, of M L to A F. Wherefore, B A being drawn, the angle refracted will be C B A, and its sine A F. But L M is the sine of the angle of inclination; and therefore again, as the density of one medium is to the density of the different medium, so reciprocally is the sine of the angle refracted to the sine of the angle of inclination; which was to be demonstrated.
In this demonstration, I have made the separating superficies B b plane by construction. But though it were concave or convex, the theorem would nevertheless be true. For the refraction being made in the point B of the plane separating superficies, if a crooked line, as P Q, be drawn, touching the separating line in the point B; neither the refracted line B I, nor the perpendicular B D, will be altered; and the refracted angle K B I, as also its sine K I, will be still the same they were.
5. The sine of the angle refracted in one inclination is to the sine of the angle refracted in another inclination, as the sine of the angle of that inclination to the sine of the angle of this inclination.
For seeing the sine of the refracted angle is to the sine of the angle of inclination, whatsoever that inclination be, as the density of one medium to the density of the other medium; the proportion of the sine of the refracted angle, to the sine of the angle of inclination, will be compounded of the proportions of density to density, and of the sine of the angle of one inclination to the sine of the angle of the other inclination. But the proportions of the densities in the same homogeneous body are supposed to be the same. Wherefore refracted angles in different inclinations are as the sines of the angles of those inclinations; which was to be demonstrated.
6. If two lines of incidence, having equal inclination, be the one in a thinner, the other in a thicker medium, the sine of the angle of their inclination will be a mean proportional between the two sines of their angles refracted.
For let the strait line A B (in fig. 3) have its inclination in the thinner medium, and be refracted in the thicker medium in B I; and let E B have as much inclination in the thicker medium, and be refracted in the thinner medium in B S; and let R S, the sine of the angle refracted, be drawn. I say, the strait lines R S, A F, and I K are in continual proportion. For it is, as the density of the thicker medium to the density of the thinner medium, so R S to A F. But it is also as the density of the same thicker medium to that of the same thinner medium, so A F to I K. Wherefore R S. A F :: A F. I K are proportionals; that is, R S, A F, and I K are in continual proportion, and A F is the mean proportional; which was to be proved.
7. If the angle of inclination be semirect, and the line of inclination be in the thicker medium, and the proportion of the densities be as that of a diagonal to the side of its square, and the separating superficies be plain, the refracted line will be in that separating superficies.
For in the circle A C (fig. 4) let the angle of inclination A B C be an angle of 45 degrees. Let C B be produced to the circumference in D; and let C E, the sine of the angle E B C, be drawn, to which let B F be taken equal in the separating line B G. B C E F will therefore be a parallelogram, and F E and B C, that is F E and B G equal. Let A G be drawn, namely the diagonal of the square whose side is B G, and it will be, as A G to E F so B G to B F; and so, by supposition, the density of the medium, in which C is, to the density of the medium in which D is; and so also the sine of the angle refracted to the sine of the angle of inclination. Drawing therefore F D, and from D the line D H perpendicular to A B produced, D H will be the sine of the angle of inclination. And seeing the sine of the angle refracted is to the sine of the angle of inclination, as the density of the medium, in which is C, is to the density of the medium in which is D, that is, by supposition, as A G is to F E, that is as B G is to D H; and seeing D H is the sine of the angle of inclination, B G will therefore be the sine of the angle refracted. Wherefore B G will be the refracted line, and lye in the plain separating superficies; which was to be demonstrated.
Coroll. It is therefore manifest, that when the inclination is greater than 45 degrees, as also when it is less, provided the density be greater, it may happen that the refraction will not enter the thinner medium at all.
8. If a body fall in a strait line upon another body, and do not penetrate it, but be reflected from it, the angle of reflection will be equal to the angle of incidence.
Let there be a body at A (in fig. 5), which falling with strait motion in the line A C upon another body at C, passeth no further, but is reflected; and let the angle of incidence be any angle, as A C D. Let the strait line C E be drawn, making with D C produced the angle E C F equal to the angle A C D; and let A D be drawn perpendicular to the strait line D F. Also in the same strait line D F let C G be taken equal to C D; and let the perpendicular G E be raised, cutting C E in E. This being done, the triangles A C D and E C G will be equal and like. Let C H be drawn equal and parallel to the strait line A D; and let H C be produced indefinitely to I. Lastly let E A be drawn, which will pass through H, and be parallel and equal to G D. I say the motion from A to C, in the strait line of incidence A C, will be reflected in the strait line C E.
For the motion from A to C is made by two coefficient or concurrent motions, the one in A H parallel to D G, the other in A D perpendicular to the same D G; of which two motions that in A H works nothing upon the body A after it has been moved as far as C, because, by supposition, it doth not pass the strait line D G; whereas the endeavour in A D, that is in H C, worketh further towards I. But seeing it doth only press and not penetrate, there will be reaction in H, which causeth motion from C towards H; and in the meantime the motion in H E remains the same it was in A H; and therefore the body will now be moved by the concourse of two motions in C H and H E, which are equal to the two motions it had formerly in A H and H C. Wherefore it will be carried on in C E. The angle therefore of reflection will be E C G, equal, by construction, to the angle A C D; which was to be demonstrated.
Now when the body is considered but as a point, it is all one whether the superficies or line in which the reflection is made be strait or crooked; for the point of incidence and reflection C is as well in the crooked line which toucheth D G in C, as in D G itself.
9. But if we suppose that not a body be moved, but some endeavour only be propagated from A to C, the demonstration will nevertheless be the same. For all endeavour is motion; and when it hath reached the solid body in C, it presseth it, and endeavoureth further in C I. Wherefore the reaction will proceed in C H; and the endeavour in C H concurring with the endeavour in H E, will generate the endeavour in C E, in the same manner as in the repercussion of bodies moved.
If therefore endeavour be propagated from any point to the concave superficies of a spherical body, the reflected line with the circumference of a great circle in the same sphere will make an angle equal to the angle of incidence.
For if endeavour be propagated from A (in fig. 6) to the circumference in B, and the centre of the sphere be C, and the line C B be drawn, as also the tangent D B E; and lastly if the angle F B D be made equal to the angle A B E, the reflection will be made in the line B F, as hath been newly shown. Wherefore the angles, which the strait lines A B and F B make with the circumference, will also be equal. But it is here to be noted, that if C B be produced howsoever to G, the endeavour in the line G B C will proceed only from the perpendicular reaction in G B; and that therefore there will be no other endeavour in the point B towards the parts which are within the sphere, besides that which tends towards the centre.
And here I put an end to the third part of this discourse; in which I have considered motion and magnitude by themselves in the abstract. The fourth and last part, concerning the phenomena of nature, that is to say, concerning the motions and magnitudes of the bodies which are parts of the world, real and existent, is that which follows.

Vol. 1. Lat. & Eng.
C. XXIV.
Fig. 1-6
| Fig 1. | Fig 2. | Fig 3. | Fig 4. | Fig 5. | Fig 6. |