6. If two bodies with uniform motion transmit two lengths, each with its own impetus and time, the proportion of the lengths transmitted will be compounded of the proportions of time to time, and impetus to impetus, directly taken.

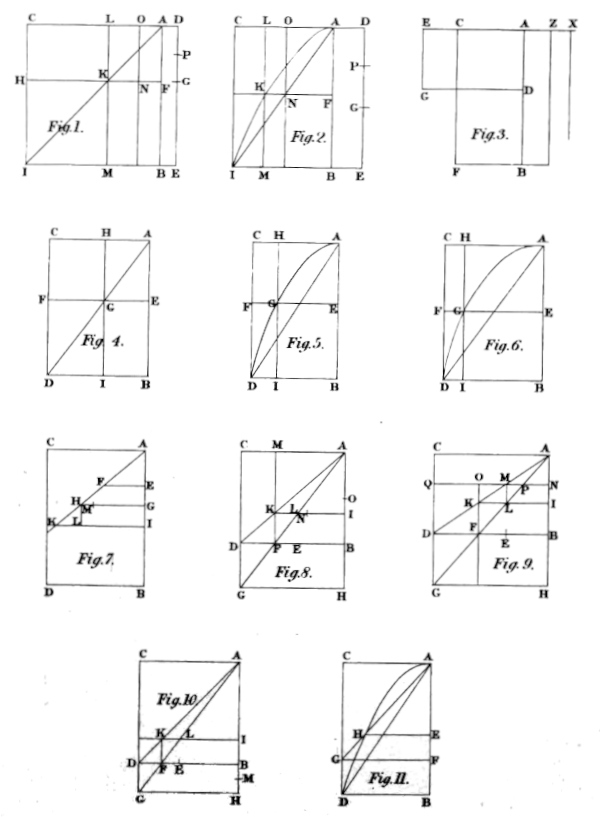
Let two bodies be moved uniformly (as in fig. 3), one in the time A B with the impetus A C, the other in the time A D with the impetus A E. I say the lengths transmitted have their proportion to one another compounded of the proportions of A B to A D, and of A C to A E. For let any length whatsoever, as Z, be transmitted by one of the bodies in the time A B with the impetus A C; and any other length, as X, be transmitted by the other body in the time A D with the impetus A E; and let the parallelograms A F and A G be completed. Seeing now Z is to X (by art. 2) as the impetus A C multiplied into the time A B is to the impetus A E multiplied into the time A D, that is, as A F to A G; the proportion of Z to X will be compounded of the same proportions, of which the proportion of A F to A G is compounded; but the proportion of A F to A G is compounded of the proportions of the side A B to the side A D, and of the side A C to the side A E (as is evident by the Elements of Euclid), that is, of the proportions of the time A B to the time A D, and of the impetus A C to the impetus A E. Wherefore also the proportion of Z to X is compounded of the same proportions of the time A B to the time A D, and of the impetus A C to the impetus A E; which was to be demonstrated.

Coroll. I. When two bodies are moved with uniform motion, if the times and impetus be in reciprocal proportion, the lengths transmitted shall be equal. For if it were as A B to A D (in the same fig. 3) so reciprocally A E to A C, the proportion of A F to A G would be compounded of the proportions of A B to A D, and of A C to A E, that is, of the proportions of A B to A D, and of A D to A B. Wherefore, A F would be to A G as A B to A B, that is, equal; and so the two products made by the multiplication of impetus into time would be equal; and by consequent, Z would be equal to X.

Coroll. II. If two bodies be moved in the same time, but with different impetus, the lengths transmitted will be as impetus to impetus. For if the time of both of them be A D, and their different impetus be A E and A C, the proportion of A G to D C will be compounded of the proportions of A E to A C and of A D to A D, that is, of the proportions of A E to A C and of A C to A C; and so the proportion of A G to D C, that is, the proportion of length to length, will be as A E to A C, that is, as that of impetus to impetus. In like manner, if two bodies be moved uniformly, and both of them with the same impetus, but in different times, the proportion of the lengths transmitted by them will be as that of their times. For if they have both the same impetus A C, and their different times be A B and A D, the proportion of A F to D C will be compounded of the proportions of A B to A D and of A C to A C; that is, of the proportions of A B to A D and of A D to A D; and therefore the proportion of A F to D C, that is, of length to length, will be the same with that of A B to A D, which is the proportion of time to time.

7. If two bodies pass through two lengths with uniform motion, the proportion of the times in which they are moved will be compounded of the proportions of length to length and impetus to impetus reciprocally taken.

For let any two lengths be given, as (in the same fig. 3) Z and X, and let one of them be transmitted with the impetus A C, the other with the impetus A E. I say the proportion of the times in which they are transmitted, will be compounded of the proportions of Z to X, and of A E, which is the impetus with which X is transmitted, to A C, the impetus with which Z is transmitted. For seeing A F is the product of the impetus A C multiplied into the time A B, the time of motion through Z will be a line, which is made by the application of the parallelogram A F to the strait line A C, which line is A B; and therefore A B is the time of motion through Z. In like manner, seeing A G is the product of the impetus A E multiplied into the time A D, the time of motion through X will be a line which is made by the application of A G to the strait line A D; but A D is the time of motion through X. Now the proportion of A B to A D is compounded of the proportions of the parallelogram A F to the parallelogram A G, and of the impetus A E to the impetus A C; which may be demonstrated thus. Put the parallelograms in order A F, A G, D C, and it will be manifest that the proportion of A F to D C is compounded of the proportions of A F to A G and of A G to D C; but A F is to D C as A B to A D; wherefore also the proportion of A B to A D is compounded of the proportions of A F to A G and of A G to D C. And because the length Z is to the length X as A F is to A G, and the impetus A E to the impetus A C as A G to D C, therefore the proportion of A B to A D will be compounded of the proportions of the length Z to the length X, and of the impetus A E to the impetus A C; which was to be demonstrated.

In the same manner it may be proved, that in two uniform motions the proportion of the impetus is compounded of the proportions of length to length and of time to time reciprocally taken.

For if we suppose A C (in the same fig. 3) to be the time, and A B the impetus with which the length Z is passed through; and A E to be the time, and A D the impetus with which the length X is passed through, the demonstration will proceed as in the last article.

8. If a body be carried by two movents together, which move with strait and uniform motion, and concur in any given angle, the line by which that body passes will be a strait line.

Let the movent A B (in fig. 4) have strait and uniform motion, and be moved till it come into the place C D; and let another movent A C, having likewise strait and uniform motion, and making with the movent A B any given angle C A B, be understood to be moved in the same time to D B; and let the body be placed in the point of their concourse, A. I say the line which that body describes with its motion is a strait line. For let the parallelogram A B D C be completed, and its diagonal A D be drawn; and in the strait line A B let any point E be taken; and from it let E F be drawn parallel to the strait lines A C and B D, cutting A D in G; and through the point G let H I be drawn parallel to the strait lines A B and C D; and lastly, let the measure of the time be A C. Seeing therefore both the motions are made in the same time, when A B is in C D, the body also will be in C D; and in like manner, when A C is in B D, the body will be in B D. But A B is in C D at the same time when A C is in B D; and therefore the body will be in C D and B D at the same time; wherefore it will be in the common point D. Again, seeing the motion from A C to B D is uniform, that is, the spaces transmitted by it are in proportion to one another as the times in which they are transmitted, when A C is in E F, the proportion of A B to A E will be the same with that of E F to E G, that is, of the time A C to the time A H. Wherefore A B will be in H I in the same time in which A C is in E F, so that the body will at the same time be in E F and H I, and therefore in their common point G. And in the same manner it will be, wheresoever the point E be taken between A and B. Wherefore the body will always be in the diagonal A D; which was to be demonstrated.

Coroll. From hence it is manifest, that the body will be carried through the same strait line A D, though the motion be not uniform, provided it have like acceleration; for the proportion of A B to A E will always be the same with that of A C to A H.

9. If a body be carried by two movents together, which meet in any given angle, and are moved, the one uniformly, the other with motion uniformly accelerated from rest, that is, that the proportion of their impetus be as that of their times, that is, that the proportion of their lengths be duplicate to that of the lines of their times, till the line of greatest impetus acquired by acceleration be equal to that of the line of time of the uniform motion; the line in which the body is carried will be the crooked line of a semiparabola, whose base is the impetus last acquired, and vertex the point of rest.

Let the straight line A B (in fig. 5) be understood to be moved with uniform motion to C D; and let another movent in the strait line A C be supposed to be moved in the same time to B D, but with motion uniformly accelerated, that is, with such motion, that the proportion of the spaces which are transmitted be always duplicate to that of the times, till the impetus acquired be B D equal to the strait line A C; and let the semiparabola A G D B be described. I say that by the concourse of those two movents, the body will be carried through the semiparabolical crooked line A G D. For let the parallelogram A B D C be completed; and from the point E, taken anywhere in the strait line A B, let E F be drawn parallel to A C and cutting the crooked line in G; and lastly, through the point G let H I be drawn parallel to the strait lines A B and C D. Seeing therefore the proportion of A B to A E is by supposition duplicate to the proportion of E F to E G, that is, of the time A C to the time A H, at the same time when A C is in E F, A B will be in H I; and therefore the moved body will be in the common point G. And so it will always be, in what part soever of A B the point E be taken. Wherefore the moved body will always be found in the parabolical line A G D; which was to be demonstrated.

10. If a body be carried by two movents together, which meet in any given angle, and are moved the one uniformly, the other with impetus increasing from rest, till it be equal to that of the uniform motion, and with such acceleration, that the proportion of the lengths transmitted be every where triplicate to that of the times in which they are transmitted; the line, in which that body is moved, will be the crooked line of the first semiparabolaster of two means, whose base is the impetus last acquired.

Let the strait line A B (in the 6th figure) be moved uniformly to C D; and let another movent A C be moved at the same time to B D with motion so accelerated, that the proportion of the lengths transmitted be everywhere triplicate to the proportion of their times; and let the impetus acquired in the end of that motion be B D, equal to the strait line A C; and lastly, let A G D be the crooked line of the first semiparabolaster of two means. I say, that by the concourse of the two movents together, the body will be always in that crooked line A G D. For let the parallelogram A B D C be completed; and from the point E, taken anywhere in the strait line A B, let E F be drawn parallel to A C, and cutting the crooked line in G; and through the point G let H I be drawn parallel to the strait lines A B and C D. Seeing therefore the proportion of A B to A E is, by supposition, triplicate to the proportion of E F to E G, that is, of the time A C to the time A H, at the same time when A C is in E F, A B will be in H I; and therefore the moved body will be in the common point G. And so it will always be, in what part soever of A B the point E be taken; and by consequent, the body will always be in the crooked line A G D; which was to be demonstrated.

11. By the same method it may be shown, what line it is that is made by the motion of a body carried by the concourse of any two movents, which are moved one of them uniformly, the other with acceleration, but in such proportions of spaces and times as are explicable by numbers, as duplicate, triplicate, &c., or such as may be designed by any broken number whatsoever. For which this is the rule. Let the two numbers of the length and time be added together; and let their sum be the denominator of a fraction, whose numerator must be the number of the length. Seek this fraction in the table of the third article of the XVIIth chapter; and the line sought will be that, which denominates the three-sided figure noted on the left hand; and the kind of it will be that, which is numbered above over the fraction. For example, let there be a concourse of two movents, whereof one is moved uniformly, the other with motion so accelerated, that the spaces are to the times as 5 to 3. Let a fraction be made whose denominator is the sum of 5 and 3, and the numerator 5, namely the fraction ⁵⁄₈. Seek in the table, and you will find ⁵⁄₈ to be the third in that row, which belongs to the three-sided figure of four means. Wherefore the line of motion made by the concourse of two such movents, as are last of all described, will be the crooked line of the third parabolaster of four means.

12. If motion be made by the concourse of two movents, whereof one is moved uniformly, the other beginning from rest in the angle of concourse with any acceleration whatsoever; the movent, which is moved uniformly, shall put forward the moved body in the several parallel spaces, less than if both the movents had uniform motion; and still less and less, as the motion of the other movent is more and more accelerated.

Let the body be placed in A, (in the 7th figure) and be moved by two movents, by one with uniform motion from the strait line A B to the strait line C D parallel to it; and by the other with any acceleration, from the strait line A C to the strait line B D parallel to it; and in the parallelogram A B D C let a space be taken between any two parallels E F and G H. I say, that whilst the movent A C passes through the latitude which is between E F and G H, the body is less moved forwards from A B towards C D, than it would have been, if the motion from A C to B D had been uniform.

For suppose that whilst the body is made to descend to the parallel E F by the power of the movent from A C towards B D, the same body in the same time is moved forwards to any point F in the line E F, by the power of the movent from A B towards C D; and let the strait line A F be drawn and produced indeterminately, cutting G H in H. Seeing therefore, it is as A E to A G, so E F to G H; if A C should descend towards B D with uniform motion, the body in the time G H, (for I make A C and its parallels the measure of time,) would be found in the point H. But because A C is supposed to be moved towards B D with motion continually accelerated, that is, in greater proportion of space to space, than of time to time, in the time G H the body will be in some parallel beyond it, as between G H and B D. Suppose now that in the end of the time G H it be in the parallel I K, and in I K let I L be taken equal to G H. When therefore the body is in the parallel I K, it will be in the point L. Wherefore when it was in the parallel G H, it was in some point between G and H, as in the point M; but if both the motions had been uniform, it had been in the point H; and therefore whilst the movent A C passes over the latitude which is between E F and G H, the body is less moved forwards from A B towards C D, than it would have been, if both the motions had been uniform; which was to be demonstrated.

13. Any length being given, which is passed through in a given time with uniform motion, to find out what length shall be passed through in the same time with motion uniformly accelerated, that is, with such motion that the proportion of the lengths passed through be continually duplicate to that of their times, and that the line of the impetus last acquired be equal to the line of the whole time of the motion.

Let A B (in the 8th figure) be a length, transmitted with uniform motion in the time A C; and let it be required to find another length, which shall be transmitted in the same time with motion uniformly accelerated, so that the line of the impetus last acquired be equal to the strait line A C.

Let the parallelogram A B D C be completed; and let B D be divided in the middle at E; and between B E and B D let B F be a mean proportional; and let A F be drawn and produced till it meet with C D produced in G; and lastly, let the parallelogram A C G H be completed. I say, A H is the length required.

For as duplicate proportion is to single proportion, so let A H be to A I, that is, let A I be the half of A H; and let I K be drawn parallel to the strait line A C, and cutting the diagonal A D in K, and the strait line A G in L. Seeing therefore A I is the half of A H, I L will also be the half of B D, that is, equal to B E; and I K equal to B F; for B D, that is, G H, B F, and B E, that is, I L, being continual proportionals, A H, A B and A I will also be continual proportionals. But as A B is to A I, that is, as A H is to A B, so is B D to I K, and so also is G H, that is, B D to B F; and therefore B F and I K are equal. Now the proportion of A H to A I is duplicate to the proportion of A B to A I, that is, to that of B D to I K, or of G H to I K. Wherefore the point K will be in a parabola, whose diameter is A H, and base G H, which G H is equal to A C. The body therefore proceeding from rest in A, with motion uniformly accelerated in the time A C, when it has passed through the length A H, will acquire the impetus G H equal to the time A C, that is, such impetus, as that with it the body will pass through the length A C in the time A C. Wherefore any length being given, &c., which was propounded to be done.

14. Any length being given, which in a given time is transmitted with uniform motion, to find out what length shall be transmitted in the same time with motion so accelerated, that the lengths transmitted be continually in triplicate proportion to that of their times, and the line of the impetus last of all acquired be equal to the line of time given.

Let the given length A B (in the 9th figure) be transmitted with uniform motion in the time A C; and let it be required to find what length shall be transmitted in the same time with motion so accelerated, that the lengths transmitted be continually in triplicate proportion to that of their times, and the impetus last acquired be equal to the time given.

Let the parallelogram A B D C be completed; and let B D be so divided in E, that B E be a third part of the whole B D; and let B F be a mean proportional between B D and B E; and let A F be drawn and produced till it meet the strait line C D in G; and lastly, let the parallelogram A C G H be completed. I say, A H is the length required.

For as triplicate proportion is to single proportion, so let A H be to another line, A I, that is, make A I a third part of the whole A H; and let I K be drawn parallel to the strait line A C, cutting the diagonal A D in K, and the strait line A G in L; then, as A B is to A I, so let A I be to another, A N; and from the point N let N Q be drawn parallel to A C, cutting A G, A D, and F K produced in P, M, and O; and last of all, let F O and L M be drawn, which will be equal and parallel to the strait lines B N and I N. By this construction, the lengths transmitted A H, A B, A I, and A N, will be continual proportionals; and, in like manner, the times G H, B F, I L and N P, that is, N Q, N O, N M and N P, will be continual proportionals, and in the same proportion with A H, A B, A I and A N. Wherefore the proportion of A H, A B, A I and A N. Wherefore the proportion of A H to A N is the same with that of B D, that is, of N Q to N P; and the proportion of N Q to N P triplicate to that of N Q to N O, that is, triplicate to that of B D to I K; wherefore also the length A H is to the length A N in triplicate proportion to that of the time B D, to the time I K; and therefore the crooked line of the first three-sided figure of two means whose diameter is A H, and base G H equal to A C, shall pass through the point O; and consequently, A H shall be transmitted in the time A C, and shall have its last acquired impetus G H equal to A C, and the proportions of the lengths acquired in any of the times triplicate to the proportions of the times themselves. Wherefore A H is the length required to be found out.

By the same method, if a length be given which is transmitted with uniform motion in any given time, another length may be found out which shall be transmitted in the same time with motion so accelerated, that the lengths transmitted shall be to the times in which they are transmitted, in proportion quadruplicate, quintuplicate, and so on infinitely. For if B D be divided in E, so that B D be to B E as 4 to 1; and there be taken between B D and B E a mean proportional F B; and as A H is to A B, so A B be made to a third, and again so that third to a fourth, and that fourth to a fifth, A N, so that the proportion of A H to A N be quadruplicate to that of A H to A B, and the parallelogram N B F O be completed, the crooked line of the first three-sided figure of three means will pass through the point O; and consequently, the body moved will acquire the impetus G H equal to A C in the time A C. And so of the rest.

15. Also, if the proportion of the lengths transmitted be to that of their times, as any number to any number, the same method serves for the finding out of the length transmitted with such impetus, and in such time.

For let A C (in the 10th figure) be the time in which a body is transmitted with uniform motion from A to B; and the parallelogram A B D C being completed, let it be required to find out a length in which that body may be moved in the same time A C from A, with motion so accelerated, that the proportion of the lengths transmitted to that of the times be continually as 3 to 2.

Let B D be so divided in E, that B D be to B E as 3 to 2; and between B D and B E let B F be a mean proportional; and let A F be drawn and produced till it meet with C D produced in G; and making A M a mean proportional between A H and A B, let it be as A M to A B, so A B to A I; and so the proportion of A H to A I will be to that of A H to A B as 3 to 2; for of the proportions, of which that of A H to A M is one, that of A H to A B is two, and that of A H to A I is three; and consequently, as 3 to 2 to that of G H to B F, and (F K being drawn parallel to B I and cutting A D in K) so likewise to that of G H or B D to I K. Wherefore the proportion of the length A H to A I is to the proportion of the time B D to I K as 3 to 2; and therefore if in the time A C the body be moved with accelerated motion, as was propounded, till it acquire the impetus H G equal to A C, the length transmitted in the same time will be A H.

16. But if the proportion of the lengths to that of the times had been as 4 to 3, there should then have been taken two mean proportionals between A H and A B, and their proportion should have been continued one term further, so that A H to A B might have three of the same proportions, of which A H to A I has four; and all things else should have been done as is already shown. Now the way how to interpose any number of means between two lines given, is not yet found out. Nevertheless this may stand for a general rule; if there be a time given, and a length be transmitted in that time with uniform motion; as for example, if the time be A C, and the length A B, the strait line A G, which determines the length C G or A H, transmitted in the same time A C with any accelerated motion, shall so cut B D in F, that B F shall be a mean proportional between B D and B E, B E being so taken in B D, that the proportion of length to length be everywhere to the proportion of time to time, as the whole B D is to its part B E.

17. If in a given time two lengths be transmitted, one with uniform motion, the other with motion accelerated in any proportion of the lengths to the times; and again, in part of the same time, parts of the same lengths be transmitted with the same motions, the whole length will exceed the other length in the same proportion in which one part exceeds the other part.

For example, let A B (in the 8th figure) be a length transmitted in the time A C, with uniform motion; and let A H be another length transmitted in the same time with motion uniformly accelerated, so that the impetus last acquired be G H equal to A C; and in A H let any part A I be taken, and transmitted in part of the time A C with uniform motion; and let another part A B be taken and transmitted in the same part of the time A C with motion uniformly accelerated; I say, that as A H is to A B, so will A B be to A I.

Let B D be drawn parallel and equal to H G, and divided in the midst at E, and between B D and B E let a mean proportional be taken as B F; and the strait line A G, by the demonstration of art. 13, shall pass through F. And dividing A H in the midst at I, A B shall be a mean proportional between A H and A I. Again, because A I and A B are described by the same motions, if I K be drawn parallel and equal to B F or A M, and divided in the midst at N, and between I K and I N be taken the mean proportional I L, the strait line A F will, by the demonstration of the same art. 13, pass through L. And dividing A B in the midst at O, the line A I will be a mean proportional between A B and A O. Where A B is divided in I and O, in like manner as A H is divided in B and I; and as A H to A B, so is A B to A I. Which was to be proved.

Coroll. Also as A H to A B, so is H B to B I; and so also B I to I O.

And as this, where one of the motions is uniformly accelerated, is proved out of the demonstration of art. 13; so, when the accelerations are in double proportion to the times, the same may be proved by the demonstration of art. 14; and by the same method in all other accelerations, whose proportions to the times are explicable in numbers.

18. If two sides, which contain an angle in any parallelogram, be moved in the same time to the sides opposite to them, one of them with uniform motion, the other with motion uniformly accelerated; that side, which is moved uniformly, will affect as much with its concourse through the whole length transmitted, as it would do if the other motion were also uniform, and the length transmitted by it in the same time were a mean proportional between the whole and the half.

Let the side A B of the parallelogram A B D C, (in the 11th figure) be understood to be moved with uniform motion till it be coincident with C D; and let the time of that motion be A C or B D. Also in the same time let the side A C be understood to be moved with motion uniformly accelerated, till it be coincident with B D; then dividing A B in the middle in E, let A F be made a mean proportional between A B and A E; and drawing F G parallel to A C, let the side A C be understood to be moved in the same time A C with uniform motion till it be coincident with F G. I say, the whole A B confers as much to the velocity of the body placed in A, when the motion of A C is uniformly accelerated till it comes to B D, as the part A F confers to the same, when the side A C is moved uniformly and in the same time to F G.

For seeing A F is a mean proportional between the whole A B and its half A E, B D will (by the 13th article) be the last impetus acquired by A C, with motion uniformly accelerated till it come to the same B D; and consequently, the strait line F B will be the excess, by which the length, transmitted by A C with motion uniformly accelerated, will exceed the length transmitted by the same A C in the same time with uniform motion, and with impetus every where equal to B D. Wherefore, if the whole A B be moved uniformly to C D in the same time in which A C is moved uniformly to F G, the part F B, seeing it concurs not at all with the motion of the side A C which is supposed to be moved only to F G, will confer nothing to its motion. Again, supposing the side A C to be moved to B D with motion uniformly accelerated, the side A B with its uniform motion to C D will less put forwards the body when it is accelerated in all the parallels, than when it is not at all accelerated; and by how much the greater the acceleration is, by so much the less it will put it forwards, as is shown in the 12th article. When therefore A C is in F G with accelerated motion, the body will not be in the side C D at the point G, but at the point D; so that G D will be the excess, by which the length transmitted with accelerated motion to B D exceeds the length transmitted with uniform motion to F G; so that the body by its acceleration avoids the action of the part A F, and comes to the side C D in the time A C, and makes the length C D, which is equal to the length A B. Wherefore uniform motion from A B to C D in the time A C, works no more in the whole length A B upon the body uniformly accelerated from A C to B D, than if A C were moved in the same time with uniform motion to F G; the difference consisting only in this, that when A B works upon the body uniformly moved from A C to F G, that, by which the accelerated motion exceeds the uniform motion, is altogether in F B or G D; but when the same A B works upon the body accelerated, that, by which the accelerated motion exceeds the uniform motion, is dispersed through the whole length A B or C D, yet, so that if it were collected and put together, it would be equal to the same F B or G D. Wherefore, if two sides which contain an angle, &c.; which was to be demonstrated.

19. If two transmitted lengths have to their times any other proportion explicable by number, and the side A B be so divided in E, that A B be to A E in the same proportion which the lengths transmitted have to the times in which they are transmitted, and between A B and A E there be taken a mean proportional A F; it may be shown by the same method, that the side, which is moved with uniform motion, works as much with its concourse through the whole length A B, as it would do if the other motion were also uniform, and the length transmitted in the same time A C were that mean proportional A F.

And thus much concerning motion by concourse.

Vol. 1. Lat. & Eng.
C. XVI.
Fig. 1-11

CHAP. XVII.

OF FIGURES DEFICIENT.

1. Definitions of a deficient figure; of a complete figure; of the complement of a deficient figure; and of proportions which are proportional and commensurable to one another.—2. The proportion of a deficient figure to its complement.—3. The proportions of deficient figures to the parallelograms in which they are described, set forth in a table.—4. The description and production of the same figures.—5. The drawing of tangents to them.—6. In what proportion the same figures exceed a strait-lined triangle of the same altitude and base.—7. A table of solid deficient figures described in a cylinder.—8. In what proportion the same figures exceed a cone of the same altitude and base.—9. How a plain deficient figure may be described in a parallelogram, so that it be to a triangle of the same base and altitude, as another deficient figure, plain or solid, twice taken, is to the same deficient figure, together with the complete figure in which it is described.—10. The transferring of certain properties of deficient figures described in a parallelogram to the proportions of the spaces transmitted with several degrees of velocity.—11. Of deficient figures described in a circle.—12. The proposition demonstrated in art. 2 confirmed from the elements of philosophy.—13. An unusual way of reasoning concerning the equality between the superficies of a portion of a sphere and a circle.—14. How from the description of deficient figures in a parallelogram, any number of mean proportionals may be found out between two given strait lines.

1. I call those deficient figures which may be understood to be generated by the uniform motion of some quantity, which decreases continually, till at last it have no magnitude at all.

And I call that a complete figure, answering to a deficient figure, which is generated with the same motion and in the same time, by a quantity which retains always its whole magnitude.

The complement of a deficient figure is that which being added to the deficient figure makes it complete.

Four proportions are said to be proportional, when the first of them is to the second as the third is to the fourth. For example, if the first proportion be duplicate to the second, and again, the third be duplicate to the fourth, those proportions are said to be proportional.

And commensurable proportions are those, which are to one another as number to number. As when to a proportion given, one proportion is duplicate, another triplicate, the duplicate proportion will be to the triplicate proportion as 2 to 3; but to the given proportion it will be as 2 to 1; and therefore I call those three proportions commensurable.

2. A deficient figure, which is made by a quantity continually decreasing to nothing by proportions everywhere proportional and commensurable, is to its complement, as the proportion of the whole altitude to an altitude diminished in any time is to the proportion of the whole quantity, which describes the figure, to the same quantity diminished in the same time.

Let the quantity A B (in fig. 1), by its motion through the altitude A C, describe the complete figure A D; and again, let the same quantity, by decreasing continually to nothing in C, describe the deficient figure A B E F C, whose complement will be the figure B D C F E. Now let A B be supposed to be moved till it lie in G K, so that the altitude diminished be G C, and A B diminished be G E; and let the proportion of the whole altitude A C to the diminished altitude G C, be, for example, triplicate to the proportion of the whole quantity A B or G K to the diminished quantity G E. And in like manner, let H I be taken equal to G E, and let it be diminished to H F; and let the proportion of G C to H C be triplicate to that of H I to H F; and let the same be done in as many parts of the strait line A C as is possible; and a line be drawn through the points B, E, F and C. I say the deficient figure A B E F C is to its complement B D C F E as 3 to 1, or as the proportion of A C to G C is to the proportion of A B, that is, of G K to G E.

For (by art. 2, chapter XV.) the proportion of the complement B E F C D to the deficient figure A B E F C is all the proportions of D B to B A, O E to E G, Q F to F H, and of all the lines parallel to D B terminated in the line B E F C, to all the parallels to A B terminated in the same points of the line B E F C. And seeing the proportions of D B to O E, and of D B to Q F &c. are everywhere triplicate of the proportions of A B to G E, and of A B to H F &c. the proportions of H F to A B, and of G E to A B &c. (by art. 16, chap. XIII.), are triplicate of the proportions of Q F to D B, and of O E to D B &c. and therefore the deficient figure A B E F C, which is the aggregate of all the lines H F, G E, A B, &c. is triple to the complement B E F C D made of all the lines Q F, O E, D B, &c.; which was to be proved.

It follows from hence, that the same complement B E F C D is ¹⁄₄ of the whole parallelogram. And by the same method may be calculated in all other deficient figures, generated as above declared, the proportion of the parallelogram to either of its parts; as that when the parallels increase from a point in the same proportion, the parallelogram will be divided into two equal triangles; when one increase is double to the other, it will be divided into a semiparabola and its complement, or into 2 and 1.

The same construction standing, the same conclusion may otherwise be demonstrated thus.

Let the strait line C B be drawn cutting G K in L, and through L let M N be drawn parallel to the strait line A C; wherefore the parallelograms G M and L D will be equal. Then let L K be divided into three equal parts, so that it may be to one of those parts in the same proportion which the proportion of A C to G C, or of G K to G L, hath to the proportion of G K to G E. Therefore L K will be to one of those three parts as the arithmetical proportion between G K and G L is to the arithmetical proportion between G K and the same G K wanting the third part of L K; and K E will be somewhat greater than a third of L K. Seeing now the altitude A G or M L is, by reason of the continual decrease, to be supposed less than any quantity that can be given; L K, which is intercepted between the diagonal B C and the side B D, will be also less than any quantity that can be given; and consequently, if G be put so near to A in g, as that the difference between C g and C A be less than any quantity that can be assigned, the difference also between C l (removing L to l) and C B, will be less than any quantity that can be assigned; and the line g l being drawn and produced to the line B D in k, cutting the crooked line in e, the proportion of G k to G l will still be triplicate to the proportion of G k to G e, and the difference between k and e, the third part of k l, will be less than any quantity that can be given; and therefore the parallelogram e D will differ from a third part of the parallelogram A e by a less difference than any quantity that can be assigned. Again, let H I be drawn parallel and equal to G E, cutting C B in P, the crooked line in F, and O E in I, and the proportion of C g to C H will be triplicate to the proportion of H F to H P, and I F will be greater than the third part of P I. But again, setting H in h so near to g, as that the difference between C h and C g may be but as a point, the point P will also in p be so near to l, as that the difference between C p and C l will be but as a point; and drawing h p till it meet with B D in i, cutting the crooked line in f and having drawn e o parallel to B D, cutting D C in o, the parallelogram f o will differ less from the third part of the parallelogram g f, than by any quantity that can be given. And so it will be in all other spaces generated in the same manner. Wherefore the differences of the arithmetical and geometrical means, which are but as so many points B, e, f, &c. (seeing the whole figure is made up of so many indivisible spaces) will constitute a certain line, such as is the line B E F C, which will divide the complete figure A D into two parts, whereof one, namely, A B E F C, which I call a deficient figure, is triple to the other, namely, B D C F E, which I call the complement thereof. And whereas the proportion of the altitudes to one another is in this case everywhere triplicate to that of the decreasing quantities to one another; in the same manner, if the proportion of the altitudes had been everywhere quadruplicate to that of the decreasing quantities, it might have been demonstrated that the deficient figure had been quadruple to its complement; and so in any other proportion. Wherefore, a deficient figure, which is made, &c. which was to be demonstrated.

The same rule holdeth also in the diminution of the bases of cylinders, as is demonstrated in the second article of chapter XV.