3. By this proposition, the magnitudes of all deficient figures, when the proportions by which their bases decrease continually are proportional to those by which their altitudes decrease, may be compared with the magnitudes of their complements; and consequently, with the magnitudes of their complete figures. And they will be found to be, as I have set them down in the following tables; in which I compare a parallelogram with three-sided figures; and first, with a strait-lined triangle, made by the base of the parallelogram continually decreasing in such manner, that the altitudes be always in proportion to one another as the bases are, and so the triangle will be equal to its complement; or the proportions of the altitudes and bases will be as 1 to 1, and then the triangle will be half the parallelogram. Secondly, with that three-sided figure which is made by the continual decreasing of the bases in subduplicate proportion to that of the altitudes; and so the deficient figure will be double to its complement, and to the parallelogram as 2 to 3. Then, with that where the proportion of the altitudes is triplicate to that of the bases; and then the deficient figure will be triple to its complement, and to the parallelogram as 3 to 4. Also the proportion of the altitudes to that of the bases may be as 3 to 2; and then the deficient figure will be to its complement as 3 to 2, and to the parallelogram as 3 to 5; and so forwards, according as more mean proportionals are taken, or as the proportions are more multiplied, as may be seen in the following table. For example, if the bases decrease so, that the proportion of the altitudes to that of the bases be always as 5 to 2, and it be demanded what proportion the figure made has to the parallelogram, which is supposed to be unity; then, seeing that where the proportion is taken five times, there must be four means; look in the table amongst the three-sided figures of four means, and seeing the proportion was as 5 to 2, look in the uppermost row for the number 2, and descending in the second column till you meet with that three-sided figure, you will find 5⁄7; which shows that the deficient figure is to the parallelogram as 5⁄7 to 1, or as 5 to 7.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |
| Parallelogram | 1 | : | : | : | : | : | : |
| Strait-sided triangle | ½ | : | : | : | : | : | : |
| Three-sided figure of 1 mean | ⅔ | : | : | : | : | : | : |
| Three-sided figure of 2 means | ¾ | ⅗ | : | : | : | : | : |
| Three-sided figure of 3 means | ⅘ | 4⁄6 | 4⁄7 | : | : | : | : |
| Three-sided figure of 4 means | 5⁄6 | 5⁄7 | 5⁄8 | 5⁄9 | : | : | : |
| Three-sided figure of 5 means | 6⁄7 | 6⁄8 | 6⁄9 | 6⁄10 | 6⁄11 | : | : |
| Three-sided figure of 6 means | 7⁄8 | 7⁄9 | 7⁄10 | 7⁄11 | 7⁄12 | 7⁄13 | : |
| Three-sided figure of 7 means | 8⁄9 | 8⁄10 | 8⁄11 | 8⁄12 | 8⁄13 | 8⁄14 | 8⁄15 |
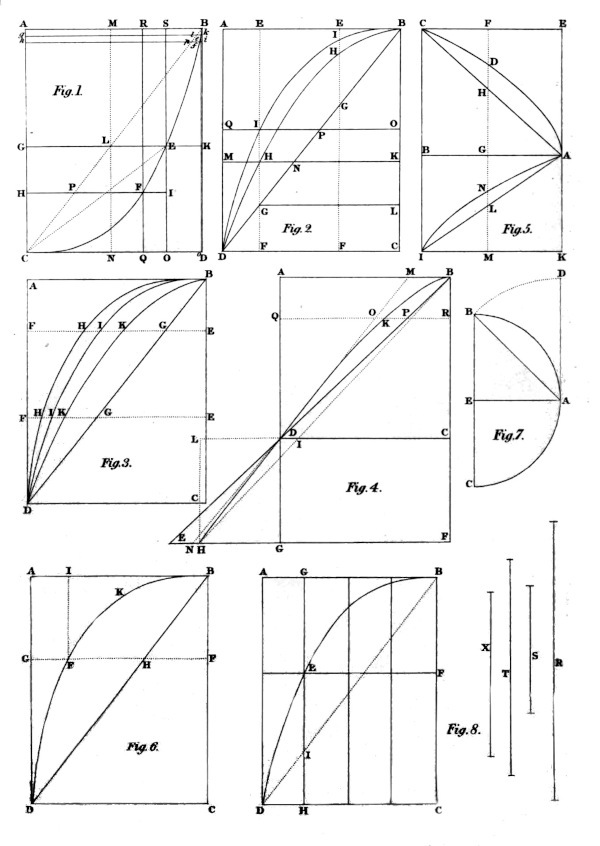
4. Now for the better understanding of the nature of these three-sided figures, I will show how they may be described by points; and first, those which are in the first column of the table. Any parallelogram being described, as A B C D (in figure 2) let the diagonal B D be drawn; and the strait-lined triangle B C D will be half the parallelogram; then let any number of lines, as E F, be drawn parallel to the side B C, and cutting the diagonal B D in G; and let it be everywhere, as E F to E G, so E G to another, E H; and through all the points H let the line B H H D be drawn; and the figure B H H D C will be that which I call a three-sided figure of one mean, because in three proportionals, as E F, E G and E H, there is but one mean, namely, E G; and this three-sided figure will be 2⁄3 of the parallelogram, and is called a parabola. Again, let it be as E G to E H, so E H to another, E I, and let the line B I I D be drawn, making the three-sided figure B I I D C; and this will be 3⁄4 of the parallelogram, and is by many called a cubic parabola. In like manner, if the proportions be further continued in E F, there will be made the rest of the three-sided figures of the first column; which I thus demonstrate. Let there be drawn strait lines, as H K and G L, parallel to the base D C. Seeing therefore the proportion of E F to E H is duplicate to that of E F to E G, or of B C to B L, that is, of C D to L G, or of K M (producing K H to A D in M) to K H, the proportion of B C to B K will be duplicate to that of K M to K H; but as B C is to B K, so is D C or K M to K N, and therefore the proportion of K M to K N is duplicate to that of K M to K H; and so it will be wheresoever the parallel K M be placed. Wherefore the figure B H H D C is double to its complement B H H D A, and consequently 2⁄3 of the whole parallelogram. In the same manner, if through I be drawn O P I Q parallel and equal to C D, it may be demonstrated that the proportion of O Q to O P, that is, of B C to B O, is triplicate that of O Q to O I, and therefore that the figure B I I D C is triple to its complement B I I D A, and consequently ¾ of the whole parallelogram, &c.
Secondly, such three-sided figures as are in any of the transverse rows, may be thus described. Let A B C D (in fig. 3) be a parallelogram, whose diagonal is B D. I would describe in it such figures, as in the preceding table I call three-sided figures of three means. Parallel to D C, I draw E F as often as is necessary, cutting B D in G; and between E F and E G, I take three proportionals E H, E I and E K. If now there be drawn lines through all the points H, I and K, that through all the points H will make the figure B H D C, which is the first of those three-sided figures; and that through all the points I, will make the figure B I D C, which is the second; and that which is drawn through all the points K, will make the figure B K D C the third of those three-sided figures. The first of these, seeing the proportion of E F to E G is quadruplicate of that E F to E H, will be to its complement as 4 to 1, and to the parallelogram as 4 to 5. The second, seeing the proportion of E F to E G is to that of E F to E I as 4 to 2, will be double to its complement, and 4⁄6 or 2⁄3 of the parallelogram. The third, seeing the proportionproportion of E F to E G is that of E F to E K as 4 to 3, will be to its complement as 4 to 3, and to the parallelogram as 4 to 7.
Any of these figures being described may be produced at pleasure, thus; let A B C D (in fig. 4) be a parallelogram, and in it let the figure B K D C be described, namely, the third three-sided figure of three means. Let B D be produced indefinitely to E, and let E F be made parallel to the base D C, cutting A D produced in G, and B C produced in F; and in G E let the point H be so taken, that the proportion of F E to F G may be quadruplicate to that of F E to F H, which may be done by making F H the greatest of three proportionals between F E and F G; the crooked line B K D produced, will pass through the point H. For if the strait line B H be drawn, cutting C D in I, and H L be drawn parallel to G D, and meeting C D produced in L; it will be as F E to F G, so C L to C I, that is, in quadruplicate proportion to that of F E to F H, or of C D to C I. Wherefore if the line B K D be produced according to its generation, it will fall upon the point H.
5. A strait line may be drawn so as to touch the crooked line of the said figure in any point, in this manner. Let it be required to draw a tangent to the line B K D H (in fig. 4) in the point D. Let the points B and D be connected, and drawing D A equal and parallel to B C, let B and A be connected; and because this figure is by construction the third of three means, let there be taken in A B three points, so, that by them the same A B be divided into four equal parts; of which take three, namely, A M, so that A B may be to A M, as the figure B K D C is to its complement. I say, the strait line M D will touch the figure in the point given D. For let there be drawn anywhere between A B and D C a parallel, as R Q, cutting the strait line B D, the crooked line B K D, the strait line M D, and the strait line A D, in the points P, K, O and Q. R K will therefore, by construction, be the least of three means in geometrical proportion between R Q and R P. Wherefore (by coroll. of art. 28, chapter XIII.) R K will be less than R O; and therefore M D will fall without the figure. Now if M D be produced to N, F N will be the greatest of three means in arithmetical proportion between F E and F G; and F H will be the greatest of three means in geometrical proportion between the same F E and F G. Wherefore (by the same coroll. of art. 28, chapter XIII.) F H will be less than F N; and therefore D N will fall without the figure, and the strait line M N will touch the same figure only in the point D.
6. The proportion of a deficient figure to its complement being known, it may also be known what proportion a strait-lined triangle has to the excess of the deficient figure above the same triangle; and these proportions I have set down in the following table; where if you seek, for example, how much the fourth three-sided figure of five means exceeds a triangle of the same altitude and base, you will find in the concourse of the fourth column with the three-sided figures of five means 2⁄10; by which is signified, that that three-sided figure exceeds the triangle by two-tenths or by one-fifth part of the same triangle.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| The triangle | 1 | : | : | : | : | : | : | ||
 |
A three-sided fig. of 1 mean | 1⁄3 | : | : | : | : | : | : | |
| The ex- cess of | A three-sided fig. of 2 means | 2⁄4 | 1⁄5 | : | : | : | : | : | |
| A three-sided fig. of 3 means | 3⁄5 | 2⁄6 | 1⁄7 | : | : | : | : | ||
| A three-sided fig. of 4 means | 4⁄6 | 3⁄7 | 2⁄8 | 1⁄9 | : | : | : | ||
| A three-sided fig. of 5 means | 5⁄7 | 4⁄8 | 3⁄9 | 2⁄10 | 1⁄11 | : | : | ||
| A three-sided fig. of 6 means | 6⁄8 | 5⁄9 | 4⁄10 | 3⁄11 | 2⁄12 | 1⁄13 | : | ||
| A three-sided fig. of 7 means | 7⁄9 | 6⁄10 | 5⁄11 | 4⁄12 | 3⁄13 | 2⁄14 | 1⁄15 |
7. In the next table are set down the proportion of a cone and the solids of the said three-sided figures, namely, the proportions between them and a cylinder. As for example, in the concourse of the second column with the three-sided figures of four means, you have 5⁄9; which gives you to understand, that the solid of the second three-sided figure of four means is to the cylinder as 5⁄9 to 1, or as 5 to 9.
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| A cylinder | 1 | : | : | : | : | : | : | ||
| A cone | 1⁄3 | : | : | : | : | : | : | ||
 |
A three-sided fig. of 1 mean | 2⁄4 | : | : | : | : | : | : | |
| A three-sided fig. of 2 means | 3⁄5 | 3⁄7 | : | : | : | : | : | ||
| The sol- ids of | A three-sided fig. of 3 means | 4⁄6 | 4⁄8 | 4⁄10 | : | : | : | : | |
| A three-sided fig. of 4 means | 5⁄7 | 5⁄9 | 5⁄11 | 5⁄13 | : | : | : | ||
| A three-sided fig. of 5 means | 6⁄8 | 6⁄10 | 6⁄12 | 6⁄14 | 6⁄16 | : | : | ||
| A three-sided fig. of 6 means | 7⁄9 | 7⁄11 | 7⁄13 | 7⁄15 | 7⁄17 | 7⁄19 | : | ||
| A three-sided fig. of 7 means | 8⁄10 | 8⁄12 | 8⁄14 | 8⁄16 | 8⁄18 | 8⁄20 | 8⁄22 |
8. Lastly, the excess of the solids of the said three-sided figures above a cone of the same altitude and base, are set down in the table which follows:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | ||||
| The Cone | 1 | : | : | : | : | : | : | |||
| The exces-ses of the sol-ids of these three- sided fig- ures above a cone. |  |
Of the solid of a three-sided figure of 1 mean | 6⁄12 | : | : | : | : | : | : | |
| Ditto ditto, 2 means | 12⁄15 | 6⁄21 | : | : | : | : | : | |||
| Ditto ditto, 3 means | 18⁄18 | 12⁄24 | 6⁄30 | : | : | : | : | |||
| Ditto ditto, 4 means | 24⁄21 | 18⁄27 | 12⁄33 | 6⁄39 | : | : | : | |||
| Ditto ditto, 5 means | 30⁄24 | 24⁄30 | 18⁄36 | 12⁄42 | 6⁄48 | : | : | |||
| Ditto ditto, 6 means | 36⁄27 | 30⁄33 | 24⁄39 | 18⁄45 | 12⁄51 | 6⁄57 | : | |||
| Ditto ditto, 7 means | 42⁄30 | 36⁄36 | 30⁄42 | 24⁄48 | 18⁄54 | 12⁄60 | 6⁄66 |
9. If any of these deficient figures, of which I have now spoken, as A B C D (in the 5th figure) be inscribed within the complete figure B E, having A D C E for its complement; and there be made upon C B produced the triangle A B I; and the parallelogram A B I K be completed; and there be drawn parallel to the strait line C I, any number of lines, as M F, cutting every one of them the crooked line of the deficient figure in D, and the strait lines A C, A B and A I in H, G, and L; and as G F is to G D, so G L be made to another, G N; and through all the points N there be drawn the line A N I: there will be a deficient figure A N I B, whose complement will be A N I K. I say, the figure A N I B is to the triangle A B I, as the deficient figure A B C D twice taken is to the same deficient figure together with the complete figure B E.
For as the proportion of A B to A G, that is, of G M to G L, is to the proportion of G M to G N, so is the magnitude of the figure A N I B to that of its complement A N I K, by the second article of this chapter.
But, by the same article, as the proportion of A B to A G, that is, of G M to G L, is to the proportion of G F to G D, that is, by construction, of G L to G N, so is the figure A B C D to its complement A D C E.
And by composition, as the proportion of G M to G L, together with that of G L to G N, is to the proportion of G M to G L, so is the complete figure B E to the deficient figure A B C D.
And by conversion, as the proportion of G M to G L is to both the proportions of G M to G L and of G L to G N, that is, to the proportion of G M to G N, which is the proportion compounded of both, so is the deficient figure A B C D to the complete figure B E.
But it was, as the proportion of G M to G L to that of G M to G N, so the figure A N I B to its complement A N I K. And therefore, A B C D. B E :: A N I B. A N I K are proportionals. And by composition, A B C D + B E. A B C D :: B K. A N I B are proportionals.
And by doubling the consequents, A B C D + B E. 2 A B C D :: B K. 2 A N I B are proportionals.
And by taking the halves of the third and the fourth, A B C D + B E. 2 A B C D :: A B I. A N I B are also proportionals; which was to be proved.
10. From what has been said of deficient figures described in a parallelogram, may be found out what proportions spaces, transmitted with accelerated motion in determined times, have to the times themselves, according as the moved body is accelerated in the several times with one or more degrees of velocity.
For let the parallelogram A B C D, in the 6th figure, and in it the three-sided figure D E B C be described; and let F G be drawn anywhere parallel to the base, cutting the diagonal B D in H, and the crooked line B E D in E; and let the proportion of B C to B F be, for example, triplicate to that of F G to F E; whereupon the figure D E B C will be triple to its complement B E D A; and in like manner, I E being drawn parallel to B C, the three-sided figure E K B F will be triple to its complement B K E I. Wherefore the parts of the deficient figure cut off from the vertex by strait lines parallel to the base, namely, D E B C and E K B F, will be to one another as the parallelograms A C and I F; that is, in proportion compounded of the proportions of the altitudes and bases. Seeing therefore the proportion of the altitude B C to the altitude B F is triplicate to the proportion of the base D C to the base F E, the figure D E B C to the figure E K B F will be quadruplicate to the proportion of the same D C to F E. And by the same method, may be found out what proportion any of the said three-sided figures has to any part of the same, cut off from the vertex by a strait line parallel to the base.
Now as the said figures are understood to be described by the continual decreasing of the base, as of C D, for example, till it end in a point, as in B; so also they may be understood to be described by the continual increasing of a point, as of B, till it acquire any magnitude, as that of C D.
Suppose now the figure B E D C to be described by the increasing of the point B to the magnitude C D. Seeing therefore the proportion of B C to B F is triplicate to that of C D to F E, the proportion of F E to C D will, by conversion, as I shall presently demonstrate, be triplicate to that B F to B C. Wherefore if the strait line B C be taken for the measure of the time in which the point B is moved, the figure E K B F will represent the sum of all the increasing velocities in the time B F; and the figure D E B C will in like manner represent the sum of all the increasing velocities in the time B C. Seeing therefore the proportion of the figure E K B F to the figure D E B C is compounded of the proportions of altitude to altitude, and base to base; and seeing the proportion of F E to C D is triplicate to that of B F to B C; the proportion of the figure E K B F to the figure D E B C will be quadruplicate to that of B F to B C; that is, the proportion of the sum of the velocities in the time B F, to the sum of the velocities in the time B C, will be quadruplicate to the proportion of B F to B C. Wherefore if a body be moved from B with velocity so increasing, that the velocity acquired in the time B F be to the velocity acquired in the time B C in triplicate proportion to that of the times themselves B F to B C, and the body be carried to F in the time B F; the same body in the time B C will be carried through a line equal to the fifth proportional from B F in the continual proportion of B F to B C. And by the same manner of working, we may determine what spaces are transmitted by velocities increasing according to any other proportions.
It remains that I demonstrate the proportion of F E to C D to be triplicate to that of B F to B C. Seeing therefore the proportion of C D, that is, of F G to F E is subtriplicate to that of B C to B F; the proportion of F G to F E will also be subtriplicate to that of F G to F H. Wherefore the proportion of F G to F H is triplicate to that of F G, that is, of C D to F E. But in four continual proportionals, of which the least is the first, the proportion of the first to the fourth, (by the 16th article of chapter XIII.), is subtriplicate to the proportion of the third to the same fourth. Wherefore the proportion of F H to G F is subtriplicate to that of F E to C D; and therefore the proportion of F E to C D is triplicate to that of F H to F G, that is, of B F to B C; which was to be proved.
It may from hence be collected, that when the velocity of a body is increased in the same proportion with that of the times, the degrees of velocity above one another proceed as numbers do in immediate succession from unity, namely, as 1, 2, 3, 4, &c. And when the velocity is increased in proportion duplicate to that of the times, the degrees proceed as numbers from unity, skipping one, as 1, 3, 5, 7, &c. Lastly, when the proportions of the velocities are triplicate to those of the times, the progression of the degrees is as that of numbers from unity, skipping two in every place, as 1, 4, 7, 10, &c., and so of other proportions. For geometrical proportionals, when they are taken in every point, are the same with arithmetical proportionals.
11. Moreover, it is to be noted that as in quantities, which are made by any magnitudes decreasing, the proportions of the figures to one another are as the proportions of the altitudes to those of the bases; so also it is in those, which are made with motion decreasing, which motion is nothing else but that power by which the described figures are greater or less. And therefore in the description of Archimedes' spiral, which is done by the continual diminution of the semidiameter of a circle in the same proportion in which the circumference is diminished, the space, which is contained within the semidiameter and the spiral line, is a third part of the whole circle. For the semidiameters of circles, inasmuch as circles are understood to be made up of the aggregate of them, are so many sectors; and therefore in the description of a spiral, the sector which describes it is diminished in duplicate proportions to the diminutions of the circumference of the circle in which it is inscribed; so that the complement of the spiral, that is, that space in the circle which is without the spiral line, is double to the space within the spiral line. In the same manner, if there be taken a mean proportional everywhere between the semidiameter of the circle, which contains the spiral, and that part of the semidiameter which is within the same, there will be made another figure, which will be half the circle. And to conclude, this rule serves for all such spaces as may be described by a line or superficies decreasing either in magnitude of power; so that if the proportions, in which they decrease, be commensurable to the proportions of the times in which they decrease, the magnitudes of the figures they describe will be known.
12. The truth of that proposition, which I demonstrated in art. 2, which is the foundation of all that has been said concerning deficient figures, may be derived from the elements of philosophy, as having its original in this; that all equality and inequality between two effects, that is, all proportion, proceeds from, and is determined by, the equal and unequal causes of those effects, or from the proportion which the causes, concurring to one effect, have to the causes which concur to the producing of the other effect; and that therefore the proportions of quantities are the same with the proportions of their causes. Seeing, therefore, two deficient figures, of which one is the complement of the other, are made, one by motion decreasing in a certain time and proportion, the other by the loss of motion in the same time; the causes, which make and determine the quantities of both the figures, so that they can be no other than they are, differ only in this, that the proportions by which the quantity which generates the figure proceeds in describing of the same, that is, the proportions of the remainders of all the times and altitudes, may be other proportions than those by which the same generating quantity decreases in making the complement of that figure, that is, the proportions of the quantity which generates the figure continually diminished. Wherefore, as the proportion of the times in which motion is lost, is to that of the decreasing quantities by which the deficient figure is generated, so will the defect or complement be to the figure itself which is generated.
13. There are also other quantities which are determinable from the knowledge of their causes, namely, from the comparison of the motions by which they are made; and that more easily than from the common elements of geometry. For example, that the superficies of any portion of a sphere is equal to that circle, whose radius is a strait line drawn from the pole of the portion to the circumference of its base, I may demonstrate in this manner. Let B A C (in fig. 7) be a portion of a sphere, whose axis is A E, and whose base is B C; and let A B be the strait line drawn from the pole A to the base in B; and let A D, equal to A B, touch the great circle B A C in the pole A. It is to be proved that the circle made by the radius A D is equal to the superficies of the portion B A C. Let the plain A E B D be understood to make a revolution about the axis A E; and it is manifest that by the strait line A D a circle will be described; and by the arch A B the superficies of a portion of a sphere; and lastly, by the subtense A B the superficies of a right cone. Now seeing both the strait line A B and the arch A B make one and the same revolution, and both of them have the same extreme points A and B, the cause why the spherical superficies, which is made by the arch, is greater than the conical superficies, which is made by the subtense, is, that A B the arch is greater than A B the subtense; and the cause why it is greater consists in this, that although they be both drawn from A to B, yet the subtense is drawn strait, but the arch angularly, namely, according to that angle which the arch makes with the subtense, which angle is equal to the angle D A B (for an angle of contingence adds nothing to an angle of a segment, as has been shown in chapter XIV, article 16.) Wherefore the magnitude of the angle D A B is the cause why the superficies of the portion, described by the arch A B, is greater than the superficies of the right cone described by the subtense A B.
Again, the cause why the circle described by the tangent A D is greater than the superficies of the right cone described by the subtense A B (notwithstanding that the tangent and the subtense are equal, and both moved round in the same time) is this, that A D stands at right angles to the axis, but A B obliquely; which obliquity consists in the same angle D A B. Seeing therefore the quantity of the angle D A B is that which makes the excess both of the superficies of the portion, and of the circle made by the radius A D, above the superficies of the right cone described by the subtense A B; it follows, that both the superficies of the portion and that of the circle do equally exceed the superficies of the cone. Wherefore the circle made by A D or A B, and the spherical superficies made by the arch A B, are equal to one another; which was to be proved.
14. If these deficient figures, which I have described in a parallelogram, were capable of exact description, then any number of mean proportionals might be found out between two strait lines given. For example, in the parallelogram A B C D, (in figure 8) let the three-sided figure of two means be described (which many call a cubical parabola); and let R and S be two given strait lines; between which, if it be required to find two mean proportionals, it may be done thus. Let it be as R to S, so B C to B F; and let F E be drawn parallel to B A, and cut the crooked line in E; then through E let G H be drawn parallel and equal to the strait line A D, and cut the diagonal B D in I; for thus we have G I the greatest of two means between G H and G E, as appears by the description of the figure in article 4. Wherefore, if it be as G H to G I, so R to another line, T, that T will be the greatest of two means between R and S. And therefore if itit be again as R to T, so T to another line, X, that will be done which was required.
In the same manner, four mean proportionals may be found out, by the description of a three-sided figure of four means; and so any other number of means, &c.
Vol. 1. Lat. & Eng.
C. XVII.
Fig. 1-8
| Fig 1. | Fig 2. | Fig 3. | Fig 4. | Fig 5. | Fig 6. | Fig 7. | Fig 8. |
CHAPTER XVIII.
OF THE EQUATION OF STRAIT LINES WITH THE
CROOKED LINES OF PARABOLAS AND OTHER
FIGURES MADE IN IMITATION OF PARABOLAS.
1. To find the strait line equal to the crooked line of a semiparabola.—2. To find a strait line equal to the crooked line of the first semiparabolaster, or to the crooked line of any other of the deficient figures of the table of the 3d article of the precedent chapter.